Một màn hình $NP$ có chiều cao $1,6$ mét được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng $NM$ bằng $1,9$ mét

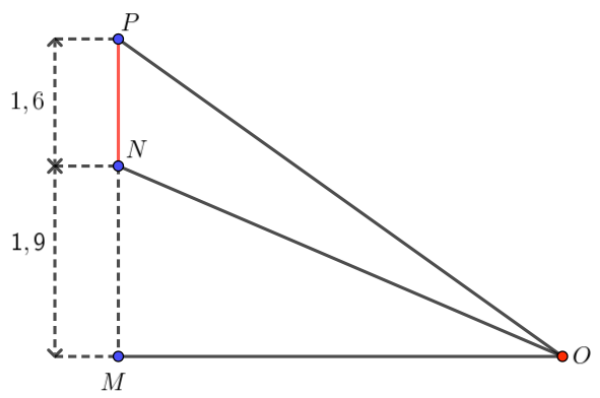
Một màn hình $NP$ có chiều cao $1,6$ mét được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng $NM$ bằng $1,9$ mét. Một chiếc đèn chiếu sáng màn hình đặt ở vị trí $O$ trên mặt đất (xem hình minh họa). Để góc chiếu sáng $\widehat{NOP}$ lớn nhất thì độ dài đoạn $OM$ bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).

Lời giải

Đáp án: 2,59

Đặt $OM=x(\text{m})$. Ta có:

$\begin{align}

& \frac{NP}{\sin \widehat{NOP}}=\frac{ON}{\sin \widehat{OPM}}\Leftrightarrow \sin \widehat{NOP}=\frac{NP.\sin \widehat{OPM}}{ON} \\

& \Rightarrow \sin \widehat{NOP}=\frac{NP.\frac{OM}{OP}}{ON}=\frac{NP.OM}{\sqrt{O{{M}^{2}}+M{{N}^{2}}}.\sqrt{O{{M}^{2}}+M{{P}^{2}}}}=\frac{1,6.x}{\sqrt{{{x}^{2}}+1,{{9}^{2}}}.\sqrt{{{x}^{2}}+3,{{5}^{2}}}} \\

\end{align}$

Xét hàm số $y=\frac{1,6x}{\sqrt{{{x}^{2}}+1,{{9}^{2}}}.\sqrt{{{x}^{2}}+3,{{5}^{2}}}}=\frac{1,6x}{\sqrt{{{x}^{4}}+15,86{{x}^{2}}+44,2225}}$

$\begin{align}

& {y}’=\frac{1,6(44,2225-{{x}^{4}})}{{{\left( \sqrt{{{x}^{4}}+15,86{{x}^{2}}+44,2225} \right)}^{3}}} \\

& {y}’=0\Leftrightarrow {{x}^{4}}=44,2225\Leftrightarrow x=\pm \frac{\sqrt{665}}{10}\approx \pm 2,59 \\

\end{align}$

Lập bảng biến thiên với điều kiện $x>0$ ta được giá trị lớn nhất của $y$ đạt được tại $x=2,59.$

Ta thấy $\widehat{NOP}$ lớn nhất khi và chỉ khi $\sin \widehat{NOP}$ lớn nhất hay $y$ lớn nhất.

Vậy $x=OM=2,59.$