Một sân điền kinh gồm hai sân hình bán nguyệt có bán kính $x\,\left( \text{m} \right)\,\,\left( x>0 \right)$ và một sân hình chữ nhật như hình vẽ

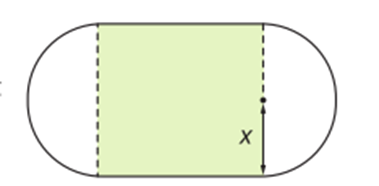
Một sân điền kinh gồm hai sân hình bán nguyệt có bán kính $x\,\left( \text{m} \right)\,\,\left( x>0 \right)$ và một sân hình chữ nhật như hình vẽ. Biết chu vi của sân điền kinh là 400 m, tìm diện tích lớn nhất của sân hình chữ nhật theo mét vuông (làm tròn kết quả đến hàng đơn vị).

Lời giải

Đáp án: 6366.

Chu vi phần hình bán nguyệt là $2\pi x$.

Độ dài cạnh còn lại của hình chữ nhật là $200-\pi x$.

Diện của sân hình chữ nhật là $S\left( x \right)=2x\left( 200-\pi x \right)=400x-2\pi {{x}^{2}}$.

${S}’\left( x \right)=400-4\pi x$.

${S}’\left( x \right)=0\Rightarrow x=\frac{100}{\pi }$.

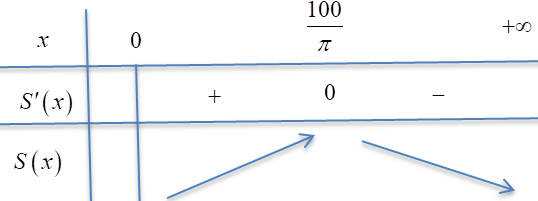
Vậy diện tích lớn nhất của hình chữ nhật là $S\left( \frac{100}{\pi } \right)\approx 6366$ ${{\text{m}}^{\text{2}}}$.