Một hình chữ nhật $ABCD$ được vẽ bên trong parabol $\left( P \right)$ sao cho $A$, $B$ thuộc $\left( P \right)$; $C$, $D$ thuộc trục $Ox$ như hình vẽ (đơn vị trên trục $Ox,Oy$ là mét)

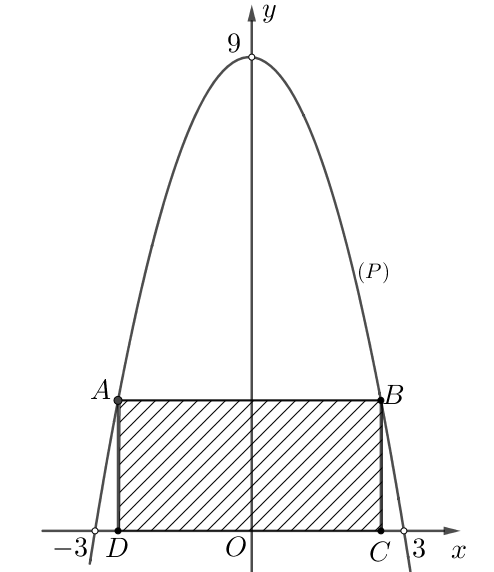
Một hình chữ nhật $ABCD$ được vẽ bên trong parabol $\left( P \right)$ sao cho $A$, $B$ thuộc $\left( P \right)$; $C$, $D$ thuộc trục $Ox$ như hình vẽ (đơn vị trên trục $Ox,Oy$ là mét). Hình chữ nhật $ABCD$ có diện tích lớn nhất là bao nhiêu mét vuông? (Kết quả làm tròn đến hàng phần mười).

Lời giải

Đáp án: $20,8$.

Đồ thị $\left( P \right)$ nhận $Oy$ làm trục đối xứng nên có phương trình $y=a{{x}^{2}}+c$.

Do $\left( P \right)$ đi qua điểm $\left( 0;9 \right)$ và $\left( 3;0 \right)$ nên ta có hệ $\left\{ \begin{align}

& c=9 \\

& 9a+c=0 \\

\end{align} \right.\Leftrightarrow \left\{ \begin{align}

& c=9 \\

& a=-1 \\

\end{align} \right.$.

Ta thu được $\left( P \right):y=-{{x}^{2}}+9$.

Giả sử $C\left( m;0 \right)$, $\left( 0<m<3 \right)$, khi đó $B\left( m;-{{m}^{2}}+9 \right)$.

Ta có $AB=2m$ và $BC=-{{m}^{2}}+9$.

Diện tích hình chữ nhật là ${{S}_{ABCD}}=AB.BC=2m\left( -{{m}^{2}}+9 \right)=-2{{m}^{3}}+18m$.

Xét hàm số $f\left( m \right)=-2{{m}^{3}}+18m$ với $m\in \left( 0;3 \right)$.

Ta có ${f}’\left( m \right)=-6{{m}^{2}}+18$, ${f}’\left( m \right)=0\Leftrightarrow -6{{m}^{2}}+18=0\Leftrightarrow m=\sqrt{3}$ (do $m>0$).

Bảng biến thiên của $f\left( m \right)$:

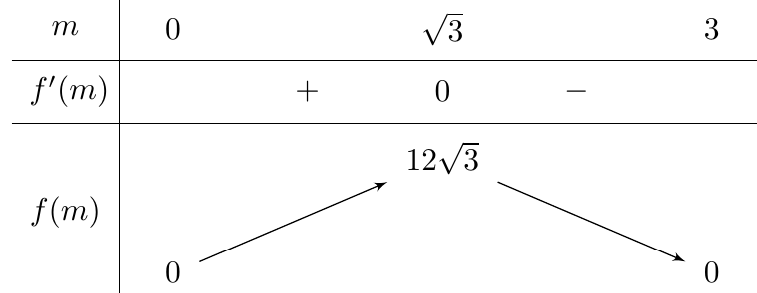
Suy ra $\max {{S}_{ABCD}}=12\sqrt{3}\approx 20,8$.

Vậy diện tích lớn nhất có thể của hình chữ nhật $ABCD$ xấp xỉ $20,8\,{{m}^{2}}$.