Giả sử số lượng tế bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số $P\left( t \right)=\frac{a}{b+{{e}^{-0,75t}}}$ (với $a,b\,\in \mathbb{R}$), trong đó thời gian $t$ được tính bằng giờ

Giả sử số lượng tế bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số $P\left( t \right)=\frac{a}{b+{{e}^{-0,75t}}}$ (với $a,b\,\in \mathbb{R}$), trong đó thời gian $t$ được tính bằng giờ. Đạo hàm của hàm số $y=P\left( t \right)$ biểu thị tốc độ sinh trưởng của nấm men (tính bằng tế bào/giờ) tại thời điểm $t$ (giờ). Tại thời điểm ban đầu $t=0$, quần thể có 20 tế bào và tốc độ sinh trưởng là 10 tế bào/giờ. Tìm số lượng tế bào của quần thể nấm men tại thời điểm tốc độ sinh trưởng của quần thể đạt mức tối đa.

Lời giải

Đáp số: 30

Theo đề bài ta có tại thời điểm ban đầu $t=0$, quần thể có 20 tế bào và tốc độ sinh trưởng là 10 tế bào/giờ suy ra $P\left( 0 \right)=20$ và ${P}’\left( 0 \right)=10$, ta có hệ phương trình sau:

$\left\{ \begin{align}

& \frac{a}{b+1}=20 \\

& \frac{0,75a}{{{\left( b+1 \right)}^{2}}}=10 \\

\end{align} \right.\Rightarrow \frac{a}{b+1}:\frac{0,75a}{{{\left( b+1 \right)}^{2}}}=20:10\Rightarrow \frac{b+1}{0,75}=2\Rightarrow b=\frac{1}{2}\Rightarrow a=30$.

Xét hàm số ${P}’\left( t \right)=\frac{0,75a\cdot {{e}^{-0,75t}}}{{{\left( b+{{e}^{-0,75t}} \right)}^{2}}}=\frac{22,5{{e}^{-0,75t}}}{{{\left( 0,5+{{e}^{-0,75t}} \right)}^{2}}},\forall t\ge 0$

Đặt $m={{e}^{-0,75t}},\,\,\forall t\ge 0\Rightarrow 0<m\le 1$.

${P}’\left( m \right)=\frac{22,5m}{{{\left( 0,5+m \right)}^{2}}}\Rightarrow {{P}’}’=\frac{-22,5{{m}^{2}}+5,625}{{{\left( 0,5+m \right)}^{4}}}=0\Leftrightarrow m=\pm \frac{1}{2}$

Bảng biến thiên

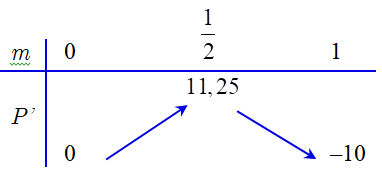
Suy ra giá trị lớn nhất của tốc độ sinh trưởng của quần thể khi $m=\frac{1}{2}\Rightarrow t=-\frac{4}{3}\ln \left( \frac{1}{2} \right)$.

Vậy số lượng tế bào của quần thể nấm men tại thời điểm $t=-\frac{4}{3}\ln \left( \frac{1}{2} \right)$ là $P=$ $30$ tế bào.