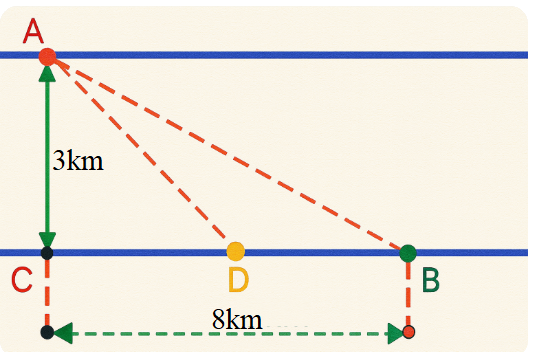
Anh An muốn di chuyển từ vị trí $A$ đến điểm $B$ càng nhanh càng tốt (như hình vẽ). Để di chuyển từ vị trí $A$ đến điểm $B$ anh An có thể chèo thuyền của mình trực tiếp qua sông để đến $C$ và sau đó chạy đến $B$, hay có thể chèo thuyền trực tiếp đến $B$, hoặc anh ta có thể chèo thuyền đến một điểm $D$ nằm giữa $B$ và $C$ sau đó chạy đến $B$. Biết anh ấy có thể chèo thuyền với vận tốc $6\text{km/h}$, chạy với vận tốc $8\text{km/h}$,$AC=3\text{km},\,\,BC=8\text{km}$ và vận tốc dòng nước là không đáng kể so với vận tốc chèo thuyền của anh An. Tìm khoảng thời gian nhanh nhất (đơn vị: giờ) để anh An đến $B$ (kết quả được làm tròn đến hàng phần trăm).
Lời giải
Đáp số: 1,33
Đặt $CD=x$$\left( km \right)$ ($0\le x\le 8$), $AD=\sqrt{9+{{x}^{2}}}$
Giả sử để đi từ $A$ đến $B$ anh An bơi thuyền từ $A$ tới $D$ sau đó chạy đến $B$.
Thời gian bơi thuyền từ $A$ tới $D$ là: $\frac{\sqrt{9+{{x}^{2}}}}{6}$, thời gian đi từ $D$ tới $B$ là: $\frac{8-x}{8}$.
Tổng thời gian là: $f\left( x \right)=\frac{\sqrt{9+{{x}^{2}}}}{6}+\frac{8-x}{8}$;
${f}’\left( x \right)=\frac{x}{6\sqrt{9+{{x}^{2}}}}-\frac{1}{8}$; ${f}’\left( x \right)=0\Leftrightarrow x=\frac{9}{\sqrt{7}}\in \left[ 0;8 \right]$.
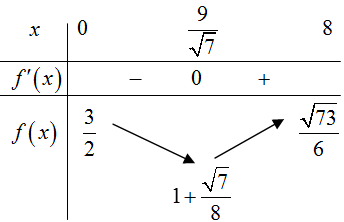
Từ bảng biến thiên, ta có $\underset{\left[ 0;8 \right]}{\mathop{\text{min}}}\,f\left( x \right)=1+\frac{\sqrt{7}}{8}$.
Vậy thời gian nhanh nhất để anh An đi từ $A$ đến $B$ là $1+\frac{\sqrt{7}}{8}\approx 1,33$.
