Khi sản xuất vỏ lon sữa DUTCH LADY, các nhà sản xuất luôn đặt tiêu chí sao cho chi phí sản xuất vỏ lon là nhỏ nhất

Khi sản xuất vỏ lon sữa DUTCH LADY, các nhà sản xuất luôn đặt tiêu chí sao cho chi phí sản xuất vỏ lon là nhỏ nhất. Biết rằng lon sữa có hình trụ và thể tích của lon sữa là $530$ $c{{m}^{3}}$. Khi diện tích toàn phần của lon sữa nhỏ nhất thì bán kính đáy của nó bằng bao nhiêu centimet? (làm tròn kết quả đến hàng phần trăm)

Lời giải

Đáp số: $4,39$.

Gọi $r$, $h$ lần lượt là bán kính đáy và chiều cao của lon sữa.

Điều kiện: $r>0$, $h>0$

+ Ta có: $V=530\Rightarrow \pi {{r}^{2}}h=530\Rightarrow h=\frac{530}{\pi {{r}^{2}}}$

+ Diện tích toàn phần của lon sữa là:

$S=2\pi rh+2\pi {{r}^{2}}=\frac{1060}{r}+2\pi {{r}^{2}}$

+ Ta có: $S’=-\frac{1060}{{{r}^{2}}}+4\pi r=0\Leftrightarrow r=\sqrt[3]{\frac{265}{\pi }}$

+ Bảng biến thiên:

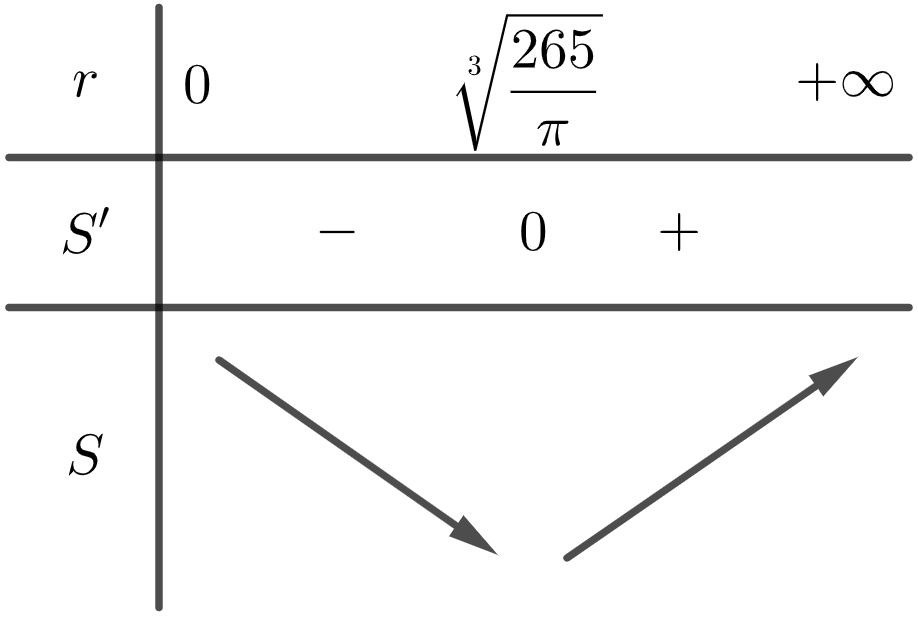
Vậy: ${{S}_{\min }}\Leftrightarrow r=\sqrt[3]{\frac{265}{\pi }}\approx 4,39$.