Ở một vịnh biển, ngoài khơi xa có một hòn đảo nhỏ

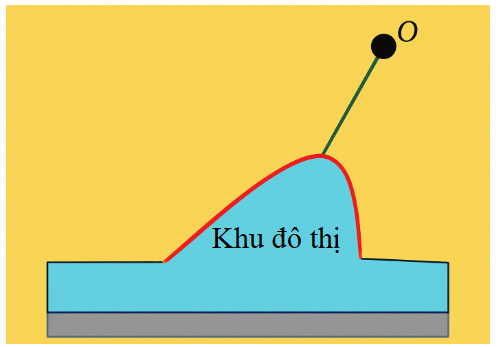
Ở một vịnh biển, ngoài khơi xa có một hòn đảo nhỏ. Người ta tiến hành lấn biển để xây dựng khu đô thị và làm một tuyến cáp treo nối khu đô thị với hòn đảo để phát triển du lịch. Xét trong hệ tọa độ ${Oxy}$ với đơn vị tương ứng 1km có hòn đảo ở ${O}$ thì đường bao của phần đất lấn biển có dạng là một phần của đồ thị hàm số $y=\frac{-{{x}^{2}}+2}{x}$. Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài của tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười)?

Lời giải

Đáp án: $1,29$

Lấy điểm $M\left( x;\frac{-{{x}^{2}}+2}{x} \right),\text{ }x\ne 0$ thuộc đồ thị $\left( C \right):y=\frac{-{{x}^{2}}+2}{x}$

Khi đó $O{{M}^{2}}={{x}^{2}}+{{\left( \frac{-{{x}^{2}}+2}{x} \right)}^{2}}=2{{x}^{2}}+\frac{4}{{{x}^{2}}}-4\ge 4\sqrt{2}-4$

Suy ra $OM\ge 2\sqrt{\sqrt{2}-1}$

Dấu $”=”$ xảy ra khi và chỉ khi $2{{x}^{2}}=\frac{4}{{{x}^{2}}}\Leftrightarrow x=\pm \sqrt{2}$

Vậy độ dài tuyến cáp treo ngắn nhất bằng $OM\ge 2\sqrt{\sqrt{2}-1}\approx 1,29$.