Một hộ gia đình chuyên làm thịt trâu sấy khô để bán, mỗi ngày hộ đó sản suất được $x$ kg thịt, $(1\le x\le 20)$

Một hộ gia đình chuyên làm thịt trâu sấy khô để bán, mỗi ngày hộ đó sản suất được $x$ kg thịt, $(1\le x\le 20)$. Tổng chi phí sản xuất $x$ kg thịt trâu khô, tính bằng nghìn đồng, cho bởi hàm chi phí: $C(x)={{x}^{3}}-9{{x}^{2}}+345x+450$. Giả sử hộ gia đình này bán hết số thịt làm ra mỗi ngày với giá $750$ nghìn đồng/kg. Gọi $L(x)$ là lợi nhuận thu được khi bán $x$ kg thịt trâu sấy khô. Hỏi lợi nhuận tối đa mà hộ gia đình này thu được trong một ngày?

Lời giải

Số tiền thu về khi bán $x$ kg thịt là: $750x$.

Lợi nhuận thu được khi bán $x$kg thịt là:$L(x)=750x-\left( {{x}^{3}}-9{{x}^{2}}+345x+450 \right)=-{{x}^{3}}+9{{x}^{2}}+405x-450$

Xét hàm số $L(x)=-{{x}^{3}}+9{{x}^{2}}+405x-450$ với $x\in [1;20]$

${L}'(x)=-3{{x}^{2}}+18x+405$; ${L}'(x)=0\Leftrightarrow \left[ \begin{align}

& x=15\in [1;20] \\

& x=-9\notin [1;20] \\

\end{align} \right.$

Bảng biến thiên

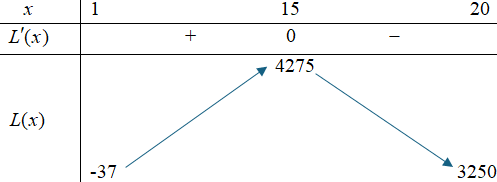
Vậy hộ gia đình sản xuất thịt khô này thu được lợi nhuận tối đa trong một ngày là $4275$ nghìn đồng khi sản xuất $15$ kg thịt trâu khô trong một ngày.