Diện tích một trang của một cuốn sách là $600c{{m}^{2}}$

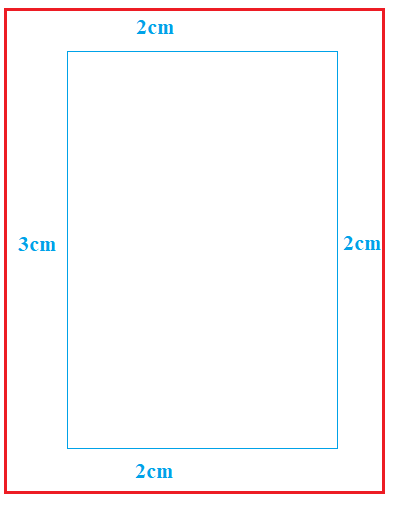
Diện tích một trang của một cuốn sách là $600c{{m}^{2}}$. Do yêu cầu kĩ thuật, cần để lề trên và lề dưới là $2cm$, lề trái là $3cm$ và lề phải là $2cm$. Tính diện tích lớn nhất của phần chữ in vào cuốn sách được (kết quả làm tròn đến hàng đơn vị)

Lời giải

Đáp án: 401

Gọi chiều dài của trang giấy là $x\,cm$ ta có chiều rộng là $\frac{600}{x}cm$.

Chiều dài và chiều rộng của phần in chữ lần lượt là $x-4$ và $\frac{600}{x}-5$

Diện tích phần in chữ là $f\left( x \right)=\left( \frac{600}{x}-5 \right)\left( x-4 \right)=620-5x-\frac{2400}{x}$

$f’\left( x \right)=\frac{2400}{{{x}^{2}}}-5=0\Leftrightarrow x=\pm 4\sqrt{30}$

Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 $c{{m}^{2}}$.