Bài toán gốc
Hàm số nào có bảng biến thiên như sau?
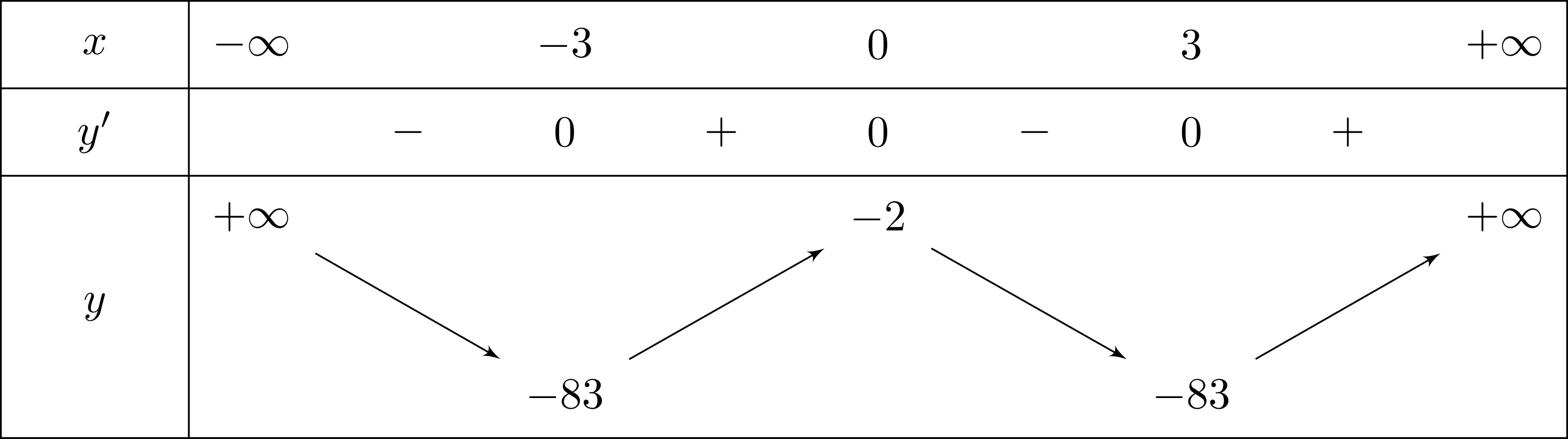
A. $y=6 x^{3} – 8 x^{2} – 2 x – 2$.B. $y=- 6 x^{3} + 8 x^{2} + 2 x + 2$.
C. $y=x^{4} – 18 x^{2} – 2$.D. $y=- x^{4} + 18 x^{2} + 2$.
Lời giải: Từ bảng biến thiên ta thấy
Bảng biến thiên của hàm số bậc bốn trùng phương dạng $y=ax^4+bx^2+c$ với $a \ne 0$.
Khoảng ngoài cùng bên phải đồng biến nên hệ số $a{>}0$ .
Phân tích và Phương pháp giải
Dạng bài toán yêu cầu nhận dạng loại hàm số (bậc ba $y=ax^3+\dots$ hoặc bậc bốn trùng phương $y=ax^4+bx^2+c$) dựa trên bảng biến thiên (BBT).
Phương pháp giải:
1. Xác định bậc của hàm số: Dựa vào số lượng cực trị (Hàm bậc ba có tối đa 2 cực trị; Hàm bậc bốn trùng phương có 1 hoặc 3 cực trị) và tập xác định ($\mathbb{R}$). BBT trong đề bài gốc chỉ ra hàm số bậc bốn trùng phương.
2. Xác định dấu của hệ số $a$ (hệ số cao nhất): Dựa vào giới hạn của hàm số khi $x \to +\infty$. Nếu $y \to +\infty$, thì $a>0$. Nếu $y \to -\infty$, thì $a<0$.
3. Kiểm tra số lượng cực trị và vị trí các điểm cực trị (nếu cần thiết để phân biệt giữa các hàm cùng bậc và cùng dấu $a$).
Bài toán tương tự
5 bài toán tương tự:
**1. Hàm số nào có bảng biến thiên thể hiện đồ thị có hình dạng chữ S ngược (hai cực trị, $y \to -\infty$ khi $x \to +\infty$)?**
| $x$ | $-\infty$ | $-1$ | $1$ | $+\infty$ |
| :—: | :—: | :—: | :—: | :—: |
| $y’$ | $-$ | $0$ | $+$ | $0$ | $-$
| $y$ | $+\infty$ | $\searrow$ | Cực tiểu | $\nearrow$ | Cực đại | $\searrow$ | $-\infty$ |
A. $y = x^3 – 3x + 1$.
B. $y = -x^3 + 3x + 1$.
C. $y = x^4 – 2x^2$.
D. $y = -x^4 + 2x^2$.
Đáp án đúng: B.
Giải thích: BBT là của hàm số bậc ba ($y=ax^3+bx^2+cx+d$) có hai cực trị. Khoảng ngoài cùng bên phải (khi $x \to +\infty$) hàm số nghịch biến, suy ra $y \to -\infty$. Do đó, hệ số $a < 0$. Chỉ có đáp án B thỏa mãn ($a=-1$). (Kiểm tra: $y' = -3x^2 + 3$, có nghiệm $x=\pm 1$).
**2. Hàm số nào có bảng biến thiên thể hiện hàm số có 3 cực trị, trong đó cực trị ở giữa là cực đại, và $y \to -\infty$ khi $x \to +\infty$?**
A. $y = x^4 – 4x^2 – 1$.
B. $y = -x^4 + 4x^2 – 1$.
C. $y = -x^3 + 4x^2 – 1$.
D. $y = x^3 – 4x^2 – 1$.
Đáp án đúng: B.
Giải thích: Hàm số có 3 cực trị phải là hàm bậc bốn trùng phương ($y=ax^4+bx^2+c$). Do $y \to -\infty$ khi $x \to +\infty$ (đồ thị có dạng chữ M), nên hệ số $a < 0$. Chỉ có đáp án B thỏa mãn ($a=-1, b=4$, $ab < 0$ nên có 3 cực trị).
**3. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:**
| $x$ | $-\infty$ | $2$ | $+\infty$ |
| :—: | :—: | :—: | :—: |
| $y’$ | $+$ | $0$ | $+$ |
| $y$ | $-\infty$ | $\nearrow$ | $f(2)$ | $\nearrow$ | $+\infty$ |
Hàm số đã cho có thể là hàm số nào trong các đáp án sau?
A. $y = x^3 – 6x^2 + 12x + 1$.
B. $y = x^3 – x$.
C. $y = -x^3 + 6x^2 – 12x + 1$.
D. $y = x^4 + 1$.
Đáp án đúng: A.
Giải thích: BBT thể hiện hàm số luôn đồng biến trên $\mathbb{R}$ và $y \to +\infty$ khi $x \to +\infty$, suy ra đây là hàm bậc ba với $a > 0$ và $y’ \ge 0$ (vô nghiệm hoặc nghiệm kép). Đáp án A có $y’ = 3x^2 – 12x + 12 = 3(x-2)^2 \ge 0$. Điểm $x=2$ là điểm uốn có tiếp tuyến nằm ngang.
**4. Hàm số nào có bảng biến thiên thể hiện chỉ có duy nhất một cực đại tại $x=0$, và $y \to -\infty$ khi $x \to \pm\infty$?**
A. $y = 3x^4 – 2x^2 + 5$.
B. $y = -x^4 – 2x^2 + 5$.
C. $y = -2x^3 + 5$.
D. $y = x^4 + 2x^2 + 5$.
Đáp án đúng: B.
Giải thích: Đây là hàm số bậc bốn trùng phương (do $y \to -\infty$ khi $x \to \pm\infty$, đồ thị dạng parabol úp ngược), suy ra $a < 0$. Hàm số chỉ có 1 cực trị (cực đại) khi $a$ và $b$ cùng dấu hoặc $b=0$. Đáp án B có $a=-1 < 0$ và $b=-2 < 0$, nên chỉ có 1 cực đại tại $x=0$.
**5. Cho hàm số có BBT thể hiện $y \to +\infty$ khi $x \to +\infty$ và có hai cực trị (Cực đại tại $x=-2$, Cực tiểu tại $x=0$). Hàm số này là hàm bậc ba nào sau đây?**
A. $y = x^3 + 3x^2 + 1$.
B. $y = x^3 – 3x + 1$.
C. $y = -x^3 – 3x^2 + 1$.
D. $y = -x^3 + 3x + 1$.
Đáp án đúng: A.
Giải thích: Đây là hàm bậc ba ($y=ax^3+bx^2+cx+d$). Do $y \to +\infty$ khi $x \to +\infty$, suy ra $a > 0$. Chỉ có A và B thỏa mãn $a>0$. Ta cần kiểm tra vị trí cực trị: $y’ = 3x^2 + 6x = 3x(x+2)$. $y’=0 \Leftrightarrow x=0$ hoặc $x=-2$. Lập BBT của A: $\dots$ Tăng (tới $x=-2$), Giảm (tới $x=0$), Tăng $\dots$. Phù hợp với Cực đại tại $x=-2$ và Cực tiểu tại $x=0$.
