Bài toán gốc
Đồ thị dưới đây là của hàm số nào?
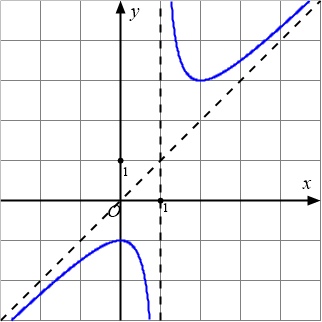
A. $y=-x^3-x^2-x-1$.B. $y=\dfrac{x-1}{x-1}$.
C. $y=x^2-4x+4$.D. $y=\dfrac{x^2-x+1}{x-1}$.
Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất.
Phân tích và Phương pháp giải
Dạng bài toán nhận dạng đồ thị hàm số. Đồ thị gốc có tiệm cận đứng và tiệm cận xiên, đặc trưng cho hàm phân thức bậc hai chia bậc nhất ($y=\dfrac{ax^2+bx+c}{dx+e}$). Phương pháp giải là loại trừ các hàm đa thức (bậc 2, bậc 3) và kiểm tra các đặc điểm tiệm cận của hàm phân thức còn lại.
Bài toán tương tự
Đồ thị dưới đây là của hàm số nào? (Giả sử đồ thị mô tả hàm số $y=\dfrac{2x+1}{x-1}$, là một hyperbol với TCĐ $x=1$ và TCN $y=2$). A. $y = x^3 – 3x$. B. $y = \dfrac{x+2}{x+1}$. C. $y = \dfrac{2x+1}{x-1}$. D. $y = x^2 – 4$. Đáp án đúng: C. Lời giải ngắn gọn: Đồ thị là một hypebol, loại trừ A và D. Hàm số có dạng $y=\dfrac{ax+b}{cx+d}$. Hàm C có tiệm cận đứng $x=1$ và tiệm cận ngang $y=2$. Hàm B có tiệm cận đứng $x=-1$ và tiệm cận ngang $y=1$. Quan sát đồ thị (giả định), nếu TCĐ là $x=1$ và TCN là $y=2$, thì C là đáp án đúng.
