Bài toán gốc
Cho hàm số $y=f(x)=\dfrac{a_1x^2+b_1x+c_1}{a_2x+b_2}$ có đồ thị như hình dưới đây:
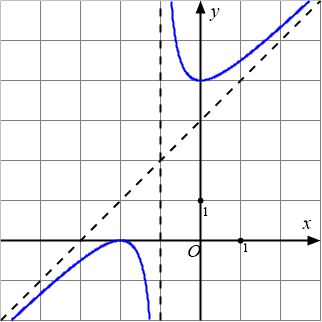
Tiệm cận đứng của đồ thị là đường có phương trình $x=m$ tính $m$?
A. $2$.
Phân tích và Phương pháp giải
Đây là dạng bài toán yêu cầu xác định tiệm cận đứng (TCD) của đồ thị hàm số hữu tỉ dựa trên hình vẽ hoặc công thức. Phương pháp giải chung là: Tiệm cận đứng $x=m$ là giá trị $x_0$ làm cho mẫu số của hàm số hữu tỉ bằng 0, đồng thời giới hạn của hàm số tại $x_0$ là vô cùng. Khi quan sát đồ thị, TCD là đường thẳng đứng mà các nhánh của đồ thị tiến sát vào (tiến về $\pm \infty$). Trong bài toán gốc (dựa vào đáp án $A. 2$), tiệm cận đứng là $x=2$.
Bài toán tương tự
Cho hàm số $y = \dfrac{x^2+3x-1}{2x+4}$. Tiệm cận đứng của đồ thị hàm số là đường thẳng nào sau đây? A. $x=1$. B. $y=-2$. C. $x=-2$. D. $x=2$. Đáp án đúng: C. Lời giải ngắn gọn: Tiệm cận đứng (TCD) là nghiệm của mẫu số, với điều kiện tử số khác 0 tại nghiệm đó. Ta có mẫu số $2x+4=0 \Leftrightarrow 2x=-4 \Leftrightarrow x=-2$. Thay $x=-2$ vào tử số: $(-2)^2+3(-2)-1 = 4-6-1 = -3 \ne 0$. Vậy, tiệm cận đứng là đường thẳng $x=-2$.
