Bài toán gốc
Cho hàm số $y=f\left( x \right)={{x}^{3}}-3x+2$ có đồ thị là $\left( C \right)$. Xét tính đúng sai của các mệnh đề sau:
a) Đồ thị $\left( C \right)$ cắt $Oy$ tại điểm nằm phía dưới trục $Ox$.
b) Đồ thị $\left( C \right)$ có hai điểm cực trị nằm về hai phía của trục $Ox$.
c) Có 5 giá trị nguyên của $m$ để phương trình ${{x}^{3}}-3x+2-m=0$ có nghiệm trên đoạn $\left[ -2;\dfrac{3}{2} \right]$.
d) Tổng các giá trị nguyên của $m\in [-10;10]$ để đồ thị hàm số $y=\dfrac{\sqrt{{{x}^{2}}+1}\left( {{x}^{2}}-4 \right)}{{{f}^{2}}\left( x \right)-m \cdot f\left( x \right)}$ chỉ có đúng hai đường tiệm cận đứng là $0$.
Lời giải: 4
(Sai) Đồ thị $\left( C \right)$ cắt $Oy$ tại điểm nằm phía dưới trục $Ox$.
(Vì): Cho $x=0$ ta được $y=2$ nên đồ thị cắt trục $Oy$ tại điểm $A\left( 0;2 \right)$ nằm phía trên trục $Ox$
(Sai) Đồ thị $\left( C \right)$ có hai điểm cực trị nằm về hai phía của trục $Ox$.
(Vì): Ta có: $y’=3{{x}^{2}}-3$.
$y’=0\Leftrightarrow x=\pm 1$.
Đồ thị hàm số có hai điểm cực trị là $M\left( -1;4 \right);N\left( 1;0 \right)$.
Ta thấy $M\left( -1;4 \right)$ nằm phía trên của $Ox$ và $N\left( 1;0 \right)$ thuộc $Ox$ nên mệnh đề sai.
(Đúng) Có 5 giá trị nguyên của $m$ để phương trình ${{x}^{3}}-3x+2-m=0$ có nghiệm trên đoạn $\left[ -2;\dfrac{3}{2} \right]$.
(Vì): Ta có: ${{x}^{3}}-3x+2-m=0\Leftrightarrow {{x}^{3}}-3x+2=m$
BBT của hàm số trên đoạn $[-2;\dfrac{3}{2}]$ là:
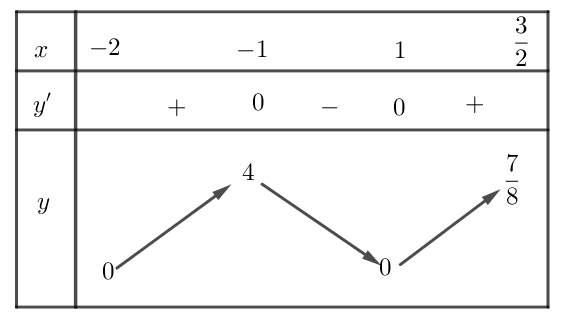
Từ BBT pt có nghiệm khi và chỉ khi $m\in [0;4]$. Mà $m\in \mathbb{Z}$ nên $m\in \{0;1;2;3;4\}$ thỏa mãn. Hay có $5$ giá trị nguyên của $m$ thỏa mãn.
Vậy mệnh đề sai.
(Sai) Tổng các giá trị nguyên của $m\in [-10;10]$ để đồ thị hàm số $y=\dfrac{\sqrt{{{x}^{2}}+1}\left( {{x}^{2}}-4 \right)}{{{f}^{2}}\left( x \right)-m \cdot f\left( x \right)}$ chỉ có đúng hai đường tiệm cận đứng là $0$.
(Vì): Xét các phương trình:
$\sqrt{{{x}^{2}}+1}\left( {{x}^{2}}-4 \right)=0\Leftrightarrow x=\pm 2$
${{f}^{2}}\left( x \right)-m \cdot f\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l} f\left( x \right)=0 \\ f\left( x \right)=m \end{array} \right]$.
Ta có BBT của hàm số:
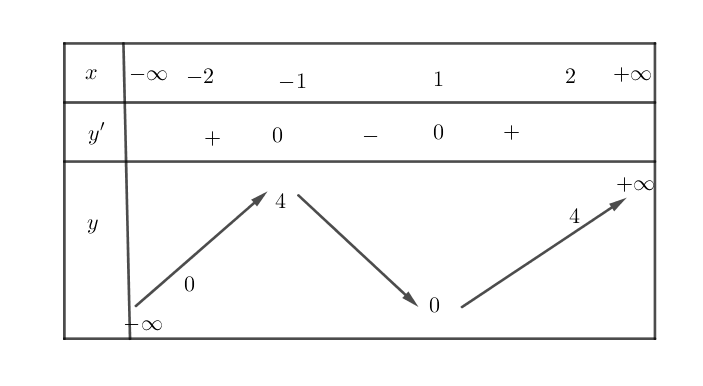
$f\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=1(\text{nghiệm kép}) \\ x=-2 \end{array} \right]$
Đường thẳng $x=-2$ không là đường tiệm cận đứng của đồ thị hàm số.
Đường thẳng $x=1$ là một đường tiệm cận đứng của đồ thị hàm số.
Căn cứ vào BBT của hàm số ta thấy đồ thị hàm số có đúng hai đường tiệm cận đứng khi và chỉ khi $\left[ \begin{array}{l} m{<}0 \\ m\ge 4 \end{array} \right]$.
Kết hợp điều kiện của $m$ ta được $m\in \{-10;-9;…..;-1;4;5;…..;10\}$. Tổng các giá trị cần tìm của $m$ là $-6.$
PHẦN III. Câu trắc nghiệm trả lời ngắn
Phân tích và Phương pháp giải
Bài toán gốc là bài toán tổng hợp kiến thức đa dạng về hàm số bậc ba, bao gồm khảo sát đồ thị (giao điểm, cực trị), giải phương trình đại số theo tham số trên đoạn, và xác định điều kiện tham số để hàm số phân thức có số lượng tiệm cận đứng cho trước. Phương pháp giải yêu cầu lập bảng biến thiên, sử dụng định nghĩa TCĐ và nguyên tắc triệt tiêu nghiệm giữa tử và mẫu (so sánh bậc nghiệm).
Bài toán tương tự
Cho hàm số $y=h\left( x \right)={{x}^{3}}-3{{x}^{2}}$ có đồ thị là $\left( C’ \right)$. Xét tính đúng sai của các mệnh đề sau:\n(a) Đồ thị $\left( C’ \right)$ cắt trục $Oy$ tại điểm nằm phía trên trục $Ox$.\n(b) Đồ thị $\left( C’ \right)$ có hai điểm cực trị nằm về hai phía khác nhau của trục $Ox$.\n(c) Có 3 giá trị nguyên của $m$ để phương trình $x^3 – 3x^2 – m = 0$ có nghiệm trên đoạn $[0; 4]$.\n(d) Tổng các giá trị nguyên của $m\in [-5;5]$ để đồ thị hàm số $y=\dfrac{\sqrt{{{x}^{2}}+1}\left( {{x}^{2}}-16 \right)}{{{h}^{2}}\left( x \right)-m \cdot h\left( x \right)}$ chỉ có đúng hai đường tiệm cận đứng là $0$.\nHỏi có bao nhiêu mệnh đề đúng trong các mệnh đề trên?\nĐáp án A: 1. Đáp án B: 2. Đáp án C: 3. Đáp án D: 4.\n\nĐáp án đúng: B\nLời giải ngắn gọn:\nHàm số $h(x) = x^3 – 3x^2$. Cực trị tại $x=0, x=2$. $h(0)=0$ (CĐ), $h(2)=-4$ (CT).\n(a) Sai. $h(0)=0$, cắt tại gốc tọa độ (trên biên $Ox$), không nằm phía trên $Ox$.\n(b) Đúng. Cực trị $(0, 0)$ và $(2, -4)$ nằm ở hai phía (hoặc trên biên) của $Ox$.\n(c) Sai. Trên $[0, 4]$, $h(x) \in [-4, 16]$. Phương trình có nghiệm khi $m \in [-4, 16]$. Có 21 giá trị nguyên.\n(d) Đúng. Tử số có nghiệm $x=\pm 4$. Mẫu số có nghiệm từ $h(x)=0$ ($x=0$ (kép), $x=3$ (đơn)) và $h(x)=m$. Phân tích điều kiện TCĐ cho thấy chỉ $m=0$ thỏa mãn yêu cầu có đúng 2 TCĐ ($x=0, x=3$). $m \in [-5, 5]$, giá trị duy nhất là $m=0$. Tổng các giá trị là 0. Mệnh đề đúng.\nVậy có 2 mệnh đề đúng là (b) và (d).
