Bài toán gốc
Cho hàm số $y=f\left( x \right)$ liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ
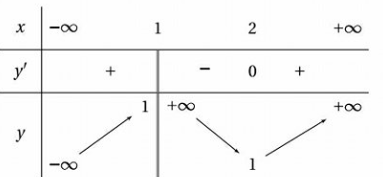
Xét tính đúng sai của các mệnh đề sau:
a) Đồ thị $\left( C \right)$ có đường tiệm cận đứng $x=1$.
b) Đồ thị $\left( C \right)$ không có đường tiệm cận ngang.
c) Đồ thị $\left( {{C}_{1}} \right):y=\dfrac{1}{f\left( x \right)}$ có không đường tiệm cận ngang.
d) Số đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{1}{{{\text{e}}^{{{f}^{2}}\left( x \right)}}-2}$ là $2$.
Lời giải: Từ BBT ta có:
$\lim\limits_{x\to {{1}^{-}}}y=+\infty ;\lim\limits_{x\to -\infty }y=\lim\limits_{x\to +\infty }y=+\infty \left( 1 \right)$
(a) Đúng.
Từ $\left( 1 \right)$ ta có TCĐ: $x=1$.
(b) Đúng.
Từ $\left( 1 \right)$ ta có đồ thị không có TCN.
(c) Sai.
Từ $\left( 1 \right)$ ta có $\lim\limits_{x\to \pm \infty }\dfrac{1}{f\left( x \right)}=0$ nên đồ thị có TCN: $y=0$.
(d) Đúng.
Xét ${{\text{e}}^{{{f}^{2}}\left( x \right)}}-2=0$ $\Leftrightarrow {{f}^{2}}\left( x \right)=\ln 2$ $\Leftrightarrow \left[ \begin{array}{l} f\left( x \right)=\sqrt{\ln 2} \\ f\left( x \right)=-\sqrt{\ln 2} \end{array} \right.$.
Dựa vào bbt ta thấy:
Đường thẳng $y=\sqrt{\ln 2}$ cắt đồ thị $y=f\left( x \right)$ tại $1$ điểm.
Đường thẳng $y=-\sqrt{\ln 2}$ cắt đồ thị $y=f\left( x \right)$ tại $1$ điểm.
Nên phương trình ${{\text{e}}^{{{f}^{2}}\left( x \right)}}-2=0$ có $2$ nghiệm phân biệt nên đồ thị hàm số $y=\dfrac{1}{{{\text{e}}^{{{f}^{2}}\left( x \right)}}-2}$ có $2$ đường tiệm cận đứng.
(Đúng) Đồ thị $\left( C \right)$ có đường tiệm cận đứng $x=1$.
(Đúng) Đồ thị $\left( C \right)$ không có đường tiệm cận ngang.
(Sai) Đồ thị $\left( {{C}_{1}} \right):y=\dfrac{1}{f\left( x \right)}$ có không đường tiệm cận ngang.
(Đúng) Số đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{1}{{{\text{e}}^{{{f}^{2}}\left( x \right)}}-2}$ là $2$.
Phân tích và Phương pháp giải
Bài toán yêu cầu xác định các đường tiệm cận (ngang và đứng) của hàm số $y=f(x)$ và các hàm hợp/phân thức chứa $f(x)$ dựa vào Bảng Biến Thiên (BBT) đã cho. Phương pháp giải bao gồm việc sử dụng định nghĩa giới hạn để xác định Tiệm cận Đứng (TCĐ, giới hạn tại điểm hữu hạn là vô cực) và Tiệm cận Ngang (TCN, giới hạn tại vô cực là hữu hạn). Đặc biệt, đối với hàm phân thức $y=1/g(x)$, TCĐ là các nghiệm đơn của mẫu số $g(x)=0$ không làm tử số bằng 0, hoặc các điểm gián đoạn của $f(x)$ khiến $g(x)\to 0$.
Bài toán tương tự
Cho hàm số $y=f(x)$ liên tục trên các khoảng xác định và có bảng biến thiên (BBT) với các giới hạn sau: $\lim_{x\to -1^-} f(x) = +\infty$, $\lim_{x\to -1^+} f(x) = 0$, $\lim_{x\to -\infty} f(x) = 2$, $\lim_{x\to +\infty} f(x) = 2$. Ngoài ra, $f(x)$ đạt giá trị cực đại là 4 (tại $x=0$). Hỏi tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=g(x) = \dfrac{1}{f^2(x) – 16}$ là bao nhiêu?A. 4; B. 3; C. 2; D. 1.Đáp án đúng: C. Lời giải ngắn gọn: 1. TCN: Ta có $\lim_{x\to \pm \infty} f(x) = 2$. Suy ra $\lim_{x\to \pm \infty} g(x) = \dfrac{1}{2^2 – 16} = -\dfrac{1}{12}$. Đồ thị có 1 TCN là $y = -1/12$. 2. TCĐ: Xét các điểm gián đoạn $x=-1$ và nghiệm của mẫu số $f^2(x) = 16$. Tại $x=-1$, $f(x) \to +\infty$, nên $g(x) \to 0$ (Không phải TCĐ). Xét $f(x) = 4$ hoặc $f(x) = -4$. Dựa vào BBT, $f(x) = 4$ có đúng 1 nghiệm đơn $x=0$. $f(x) = -4$ vô nghiệm (vì giá trị nhỏ nhất của $f(x)$ là 0). Đồ thị có 1 TCĐ là $x=0$. Tổng số đường tiệm cận là $1 + 1 = 2$.
