Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -2 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

Bài toán gốc

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -2 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

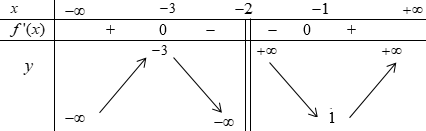
Các mệnh đề sau đúng hay sai?

a) Hàm số đạt cực đại tại điểm $x=-3$ và đạt cực tiểu tại $x=-1$.

b) Đồ thị hàm số nhận đường thẳng $y=-2$ làm tiệm cận đứng.

c) Hàm số nghịch biến trên khoảng $\left( -3;-1 \right)$.

d) Đồ thị hàm số không có điểm chung với trục hoành.

Lời giải: a) Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại điểm $x=-3$ và đạt cực tiểu tại $x=-1$. Chọn Đ
Từ bảng biến thiên ta có: $\max\limits_{x\to {{(-2)}^{+}}}f(x)=+\infty$ và $\min\limits_{x\to {{(-2)}^{-}}}f(x)=-\infty$ nên đồ thị hàm số nhận đường thẳng $x=-2$ làm tiệm cận đứng. Chọn Đ
Từ bảng biến thiên ta có: Hàm số nghịch biến trên khoảng $\left( -3;-2 \right)$ và $\left( -2;-1 \right)$. Hàm số không xác định tại $x=-2$. Chọn S
Từ bảng biến thiên ta có: $f(x)=0$ vô nghiệm nên đồ thị hàm số không có điểm chung với trục hoành. Chọn Đ
(Đúng) Hàm số đạt cực đại tại điểm $x=-3$ và đạt cực tiểu tại $x=-1$.
(Vì): Từ bảng biến thiên ta thấy hàm số đạt cực đại tại $x=-3$ và đạt cực tiểu tại $x=-1$.
(Sai) Đồ thị hàm số nhận đường thẳng $y=-2$ làm tiệm cận đứng.
(Vì): Từ bảng biến thiên ta có: $\lim\limits_{x\to {{(-2)}^{+}}}f(x)=+\infty$ và $\lim\limits_{x\to {{(-2)}^{-}}}f(x)=-\infty$ nên đồ thị hàm số nhận đường thẳng $x=-2$ làm tiệm cận đứng.
(Sai) Hàm số nghịch biến trên khoảng $\left( -3;-1 \right)$.
(Vì): Từ bảng biến thiên ta có: Hàm số nghịch biến trên khoảng $\left( -3;-2 \right)$ và $\left( -2;-1 \right)$. Do hàm số không xác định tại $x=-2$ nên không nghịch biến trên $\left( -3;-1 \right)$.
(Đúng) Đồ thị hàm số không có điểm chung với trục hoành.
(Vì): Từ bảng biến thiên ta có $f(x) \le -3$ với mọi $x \in (-\infty; -2)$ và $f(x) \ge 1$ với mọi $x \in (-2; +\infty)$. Do đó phương trình $f(x)=0$ vô nghiệm, tức đồ thị hàm số không có điểm chung với trục hoành.

Phân tích và Phương pháp giải

Đây là dạng bài tập phân tích các tính chất cơ bản của hàm số (cực trị, tính đơn điệu, tiệm cận, giao điểm với trục hoành) thông qua việc đọc hiểu bảng biến thiên. Phương pháp giải đòi hỏi sự chính xác trong việc diễn giải các thông tin từ bảng: giới hạn (tiệm cận), dấu của đạo hàm (đơn điệu), sự thay đổi dấu của đạo hàm (cực trị) và tập giá trị của hàm số (giao điểm với trục hoành). Cần đặc biệt lưu ý đến các điểm gián đoạn khi xét tính đơn điệu trên một khoảng lớn hơn các khoảng xác định.

Bài toán tương tự

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\backslash \left\{ 1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:\n\n| $x$ | $-\infty$ | $0$ | $1$ (||) | $2$ | $+\infty$ |\n|—|—|—|—|—|—|\n| $y’$ | $+$ | $0$ | $-$ | (||) | $-$ | $0$ | $+$ |\n| $y$ | $3 \to 5$ | $5 \to -\infty$ | (||) | $+\infty \to 4$ | $4 \to 3$ |\n\nMệnh đề nào sau đây là SAI?\nA. Hàm số có hai tiệm cận ngang.\nB. Hàm số đạt cực đại tại $x=0$.\nC. Hàm số nghịch biến trên khoảng $(0; 1)$.\nD. Phương trình $f(x)=m$ có ít nhất 2 nghiệm phân biệt khi $4 < m < 5$.\n\nĐáp án đúng: A\nLời giải ngắn gọn: \n- Tiệm cận ngang: Ta có $\lim_{x\to -\infty} f(x) = 3$ và $\lim_{x\to +\infty} f(x) = 3$. Đồ thị hàm số chỉ có MỘT tiệm cận ngang là $y=3$. Mệnh đề A là SAI.\n- Tiệm cận đứng: $\lim_{x\to 1^-} f(x) = -\infty$ và $\lim_{x\to 1^+} f(x) = +\infty$. Tiệm cận đứng là $x=1$.\n- Cực trị: Tại $x=0$, $y'$ đổi dấu từ $+$ sang $-$ nên hàm số đạt cực đại tại $x=0$. (B đúng).\n- Đơn điệu: Trên khoảng $(0; 1)$, $y' < 0$ nên hàm số nghịch biến. (C đúng).\n- Số nghiệm: Khi $4 < m < 5$, đường thẳng $y=m$ cắt nhánh trái tại 1 điểm (do $3