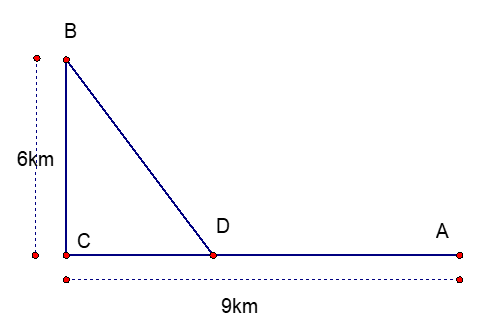
Một công ty muốn xây dựng hệ thống dây cáp từ trạm A ở trên bờ biển đến một vị trí B trên một hòn đảo. Hòn đảo cách bờ biển 6 km. Gọi C là điểm trên bờ sao cho BC vuông góc với bờ biển. Khoảng cách từ A đến C là 9 km. Giá để lắp đặt mỗi km hệ thống dây trên bờ là 50 triệu đồng và dưới nước là 130 triệu đồng. Người ta cần xác định một vị trí D trên AC để lắp đặt hệ thống dây theo đường gấp khúc ADB mà số tiền chi phí thấp nhất. Khi đó chi phí lắp đặt thấp nhất là bao nhiêu triệu đồng?
Đáp án: 1170
Lời giải: Đặt $CD=x$ (km) $\left( x\in \left[ 0;9 \right] \right)$
Ta có $AD=9-x$ (km) và $BD=\sqrt{C{{D}^{2}}+B{{C}^{2}}}=\sqrt{{{x}^{2}}+36}$ (km).
Chi phí lắp đặt là: $F\left( x \right)=50\left( 9-x \right)+130\sqrt{{{x}^{2}}+36}$ (triệu đồng).
Xét hàm số $F\left( x \right)=50\left( 9-x \right)+130\sqrt{{{x}^{2}}+36}$ trên $\left[ 0;9 \right]$
${F}’\left( x \right)=-50+\dfrac{130x}{\sqrt{{{x}^{2}}+36}}$.
${F}’\left( x \right)=0\Leftrightarrow \dfrac{130x}{\sqrt{{{x}^{2}}+36}}-50=0\Leftrightarrow 13x=5\sqrt{{{x}^{2}}+36}$ $\Leftrightarrow \left\{ \begin{array}{l} x\ge 0 \\ 169{{x}^{2}}=25\left( {{x}^{2}}+36 \right) \end{array} \right.\Leftrightarrow x=\dfrac{5}{2}(\text{tm})$
BBT:
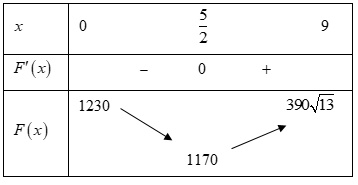
Vậy chi phí thấp nhất để lắp đặt hệ thống dây cáp là $1170$ triệu đồng.
