Một công ty muốn làm một đường ống dẫn từ vị trí $A$ trên bờ biển đến vị trí $B$ trên hòn đảo

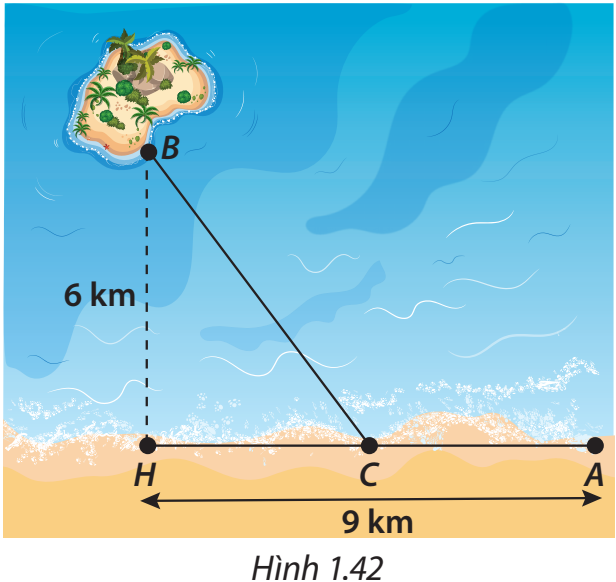
Một công ty muốn làm một đường ống dẫn từ vị trí $A$ trên bờ biển đến vị trí $B$ trên hòn đảo. Khoảng cách từ điểm $B$ đến bờ biển là $BH=6km$ (Hình 1.42). Giá tiền để xây dựng đường ống trên bờ là $50000$ USD trên mỗi kilomet và giá tiền xây dựng đường ống trên biển là $130000$ USD mỗi kilomet, biết rằng $AH=9km$. Xác định vị trí điểm $C$ trên đoạn $AH$ để khi lắp ống dẫn theo đường gấp khúc $ACB$ thì chi phí công ty bỏ ra là thấp nhất.

Đáp án: 2,5

Lời giải: Gọi $HC=x\left( km,0{<}x{
Chi phí lắp ống của công ty là $50000\left( 9-x \right)+130000\sqrt{36+{{x}^{2}}}$.
Ta đặt $f\left( x \right)=50000\left( 9-x \right)+130000\sqrt{36+{{x}^{2}}}$.
Tập xác định $D=\mathbb{R}$.
Ta có: $f’\left( x \right)=-50000+130000.\dfrac{x}{\sqrt{36+{{x}^{2}}}}$.
Xét $f’\left( x \right)=0$
$\begin{array}{l} \Leftrightarrow -50000+130000.\dfrac{x}{\sqrt{36+{{x}^{2}}}}=0 \\ \Leftrightarrow \dfrac{x}{\sqrt{36+{{x}^{2}}}}=\dfrac{5}{13}\Leftrightarrow 13x=5\sqrt{36+{{x}^{2}}}\Leftrightarrow 169{{x}^{2}}=900+25{{x}^{2}}\Leftrightarrow \left[ \begin{array}{l} x=\dfrac{5}{2} \\ x=\dfrac{-5}{2} \end{array} \right. \end{array}$
Bảng biến thiên:

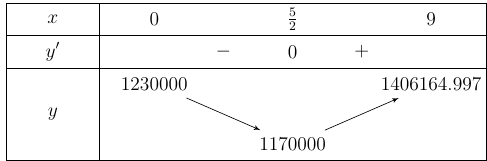
Từ bảng biến thiên, ta thấy hàm số đạt giá trị nhỏ nhất khi $x=\dfrac{5}{2}$.
Vậy để chi phí lắp đặt nhỏ nhất thì điểm $C$ cách điểm $H$ một khoảng $2,5$ km.