Từ một miếng tôn dạng nửa hình tròn có bán kính $R=4$ dm, người ta muốn cắt ra một hình chữ nhật

Từ một miếng tôn dạng nửa hình tròn có bán kính $R=4$ dm, người ta muốn cắt ra một hình chữ nhật. Hỏi diện tích lớn nhất của hình chữ nhật có thể cắt được là bao nhiêu?
Đáp án: 16

Lời giải:

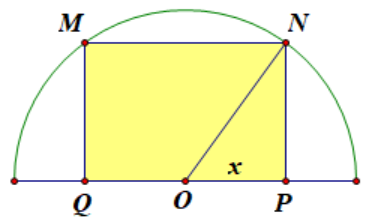
Gọi hình chữ nhật cần tính diện tích là $MNPQ$ có $OP=x$ $\left( 0{<}x{
Khi đó diện tích của hình chữ nhật $MNPQ$ là: $S=MN.NP$ $=2x\sqrt{16-{{x}^{2}}}$.
Xét hàm số : $f\left( x \right)=2x\sqrt{16-{{x}^{2}}}$ trên $\left( 0;4 \right)$.
Ta có : ${f}’\left( x \right)=2\sqrt{16-{{x}^{2}}}-\dfrac{2{{x}^{2}}}{\sqrt{16-{{x}^{2}}}}$ $=\dfrac{-4{{x}^{2}}+32}{\sqrt{16-{{x}^{2}}}}$; ${f}’\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=2\sqrt{2}\in \left( 0;4 \right) \\ x=-2\sqrt{2}\notin \left( 0;4 \right) \end{array} \right.$.
BBT:

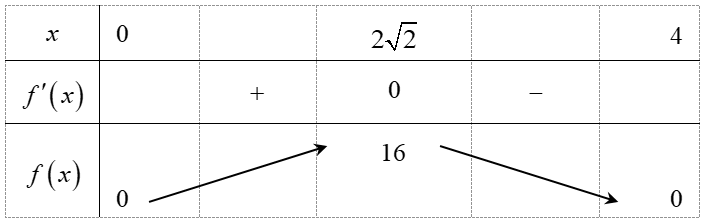
Ta có: $\max\limits_{\left( 0;4 \right)}f\left( x \right)=f\left( 2\sqrt{2} \right)=16$.
Vậy diện tích lớn nhất của hình chữ nhật có thể cắt được là $16\text{(d}{{\text{m}}^{\text{2}}}\text{)}$.