Cho một bờ sông hình bán nguyệt có bán kính bằng $2km$, đường kính $PR$ như hình vẽ sau:

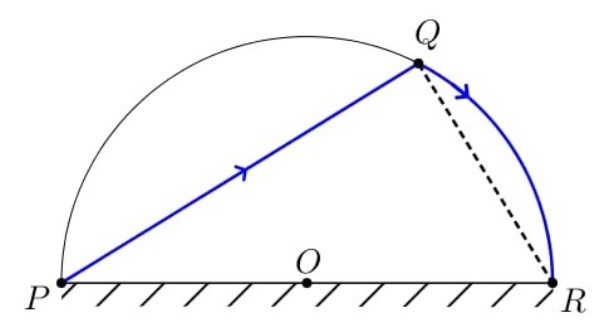
Từ điểm $P$ anh Tèo chèo một chiếc thuyền với vận tốc $3km/h$ đến điểm $Q$ trên bờ hồ, rồi chạy bộ dọc theo thành hồ đến vị trí $R$ với vận tốc $6km/h$. Thời gian lớn nhất mà anh Tèo di chuyển từ $P$ đến $R$ là bao nhiêu? (thời gian tính bằng giờ, kết quả làm tròn đến phần chục)
Đáp án: 1,5

Lời giải:

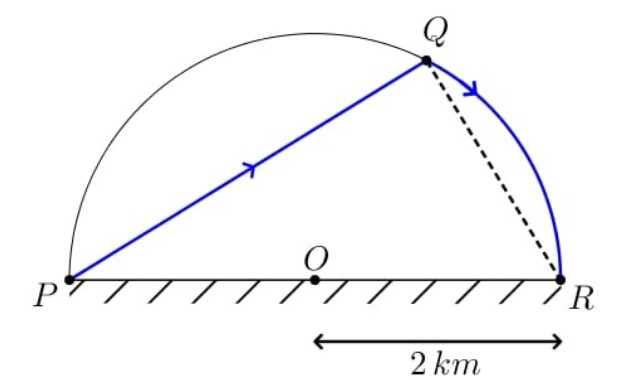
Đặt $\widehat{QPR}=\alpha (rad)$, $\alpha \in \left( 0;\dfrac{\pi }{2} \right)$.
Ta có $\Delta PQR$ vuông tại $Q$ $\Rightarrow PQ=PR.\text{cos}\alpha \text{=4cos}\alpha$ mà $\widehat{OQR}=2.\widehat{QPR}=2\alpha$.
Độ dài cung tròn $QR=2.2\alpha =4\alpha$.
Thời gian anh Tèo chèo thuyền từ $P$ đến $Q$ là $\dfrac{4\cos \alpha }{3}$ (giờ)
Thời gian anh Tèo chèo từ $Q$ đến $R$ là $\dfrac{4\alpha }{6}=\dfrac{2\alpha }{3}$ (giờ)
Tổng thời gian anh Tèo di chuyển từ $P$ đến $R$ là $t=\dfrac{4\cos \alpha }{3}+\dfrac{2\alpha }{3},\left( 0{
Xét hàm số $t\left( \alpha \right)=\dfrac{4\cos \alpha }{3}+\dfrac{2\alpha }{3}$ với $\alpha \in \left( 0;\dfrac{\pi }{2} \right)$.
${t}’\left( \alpha \right)=\dfrac{1}{3}\left( -4\sin \alpha +2 \right)$, $\alpha \in \left( 0;\dfrac{\pi }{2} \right)$
${t}’\left( \alpha \right)=0\Leftrightarrow \sin \alpha =\dfrac{1}{2}\Rightarrow \alpha =\dfrac{\pi }{6}$
Bảng biến thiên Tìm được $t\left( \alpha \right)\le t\left( \dfrac{\pi }{6} \right)\approx 1,5$ (giờ)

Reader Interactions

Để lại một bình luận Hủy