Một màn hình chữ nhật cao $1,4\text{m}$ và đặt ở độ cao $1,8\text{m}$ so với tầm mắt (tính từ đầu mép dưới của màn hình như hình vẽ bên dưới)

Một màn hình chữ nhật cao $1,4\text{m}$ và đặt ở độ cao $1,8\text{m}$ so với tầm mắt (tính từ đầu mép dưới của màn hình như hình vẽ bên dưới).

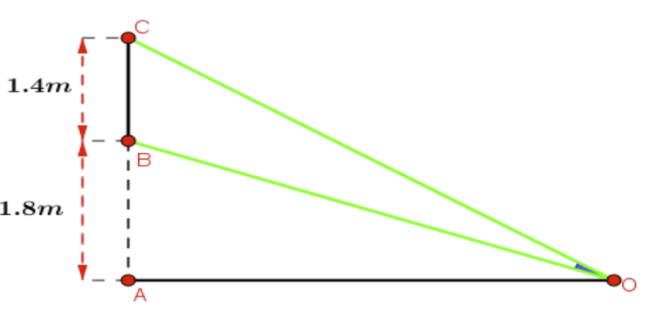
Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn nhất. Tính khoảng cách từ vị trí đó đến màn hình? Biết rằng góc $\widehat{BOC}$ nhọn.
Đáp án: 2,4

Lời giải: Đặt độ dài $OA=x\left( \text{m} \right)$ với $x{>}0$. Ta có: $OB=\sqrt{{{x}^{2}}+3,24}$; $OC=\sqrt{{{x}^{2}}+10,24}$
Sử dụng định lí cosin trong tam giác $OBC$ :
$\cos \widehat{BOC}=\dfrac{O{{B}^{2}}+O{{C}^{2}}-B{{C}^{2}}}{2.OB.OC}=\dfrac{{{x}^{2}}+3,24+{{x}^{2}}+10,24-1.96}{2\sqrt{{{x}^{2}}+3,24}.\sqrt{{{x}^{2}}+10,24}}$
$=\dfrac{{{x}^{2}}+5,76}{\sqrt{\left( {{x}^{2}}+3,24 \right)\left( {{x}^{2}}+10,24 \right)}}$.
Vì góc $\widehat{BOC}$ nhọn nên $\widehat{BOC}$ lớn nhất khi và chỉ khi $\cos \widehat{BOC}$ nhỏ nhất. Khi đó bài toán trở thành tìm $x$ để $f\left( x \right)=\dfrac{{{x}^{2}}+5,76}{\sqrt{\left( {{x}^{2}}+3,24 \right)\left( {{x}^{2}}+10,24 \right)}}$ đạt giá trị nhỏ nhất.
Đặt $t={{x}^{2}}+3,24$ với $t{>}3,24$. Suy ra $f\left( t \right)=\dfrac{t+\dfrac{63}{25}}{\sqrt{t\left( t+7 \right)}}$ với $t\in \left( 3,24;+\infty \right)$.
Ta có: ${f}’\left( t \right)=\dfrac{1}{25}\left( \dfrac{49t-441}{2t\left( t+7 \right)\sqrt{t\left( t+7 \right)}} \right)$.
Cho ${f}’\left( x \right)=0\Leftrightarrow 49t-441=0\Leftrightarrow t=9$.
Bảng biến thiên:

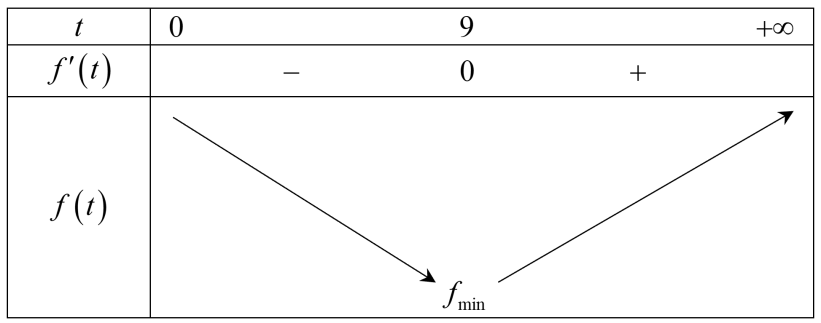
Thế vào biểu thức của phép đặt ta có: ${{x}^{2}}+3,24=9\Leftrightarrow {{x}^{2}}=\dfrac{144}{25}\Rightarrow x=2,4\text{m}$.
Vậy để nhìn rõ nhất thì khoảng cách từ vị trí đó đến màn hình là $OA=2,4\text{m}$.