Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ)

Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết $a=24$ và $b=3$. Hỏi cái sào thảo mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu? (làm tròn kết quả đến hàng phần mười)

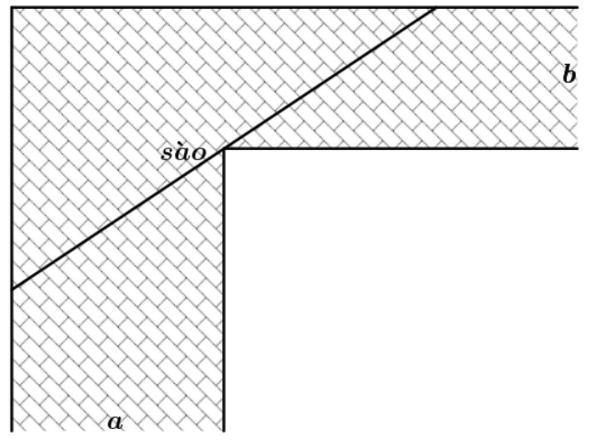
Đáp án: 1125

Lời giải:

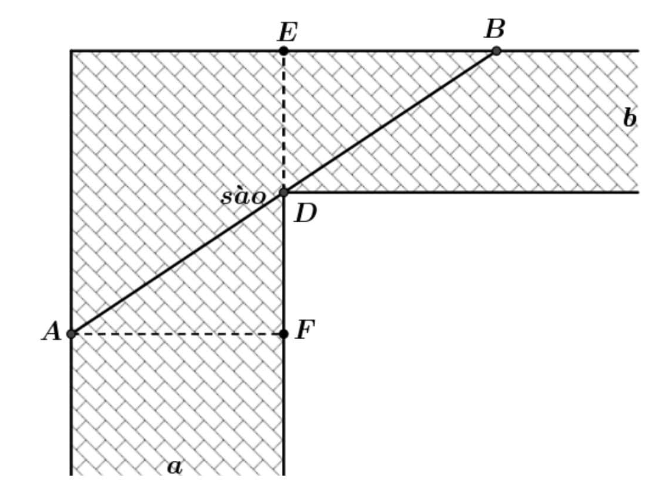
Đặt các điểm như hình vẽ
Đặt $DF=x,x{>}0,$ ta có $\Delta ADF$ đồng dạng với $\Delta BED$ nên $\dfrac{EB}{ED}=\dfrac{AF}{DF}\Rightarrow EB=\dfrac{ab}{x}$
Gọi $l$ là chiều dài của que sào, ta có ${{l}^{2}}=A{{B}^{2}}={{\left( x+b \right)}^{2}}+{{\left( a+\dfrac{ab}{x} \right)}^{2}}=f\left( x \right)$
Đạo hàm ${f}’\left( x \right)=2\left( x+b \right)-2\dfrac{ab}{{{x}^{2}}}{{\left( a+\dfrac{ab}{x} \right)}^{2}}=2\left( x+b \right)\left( 1-\dfrac{{{a}^{2}}b}{{{x}^{3}}} \right);{f}’\left( x \right)=0\Leftrightarrow x=\sqrt[3]{{{a}^{2}}b}=12$
Dễ dàng suy ra được $\min\limits_{\left( 0;+\infty \right)}f\left( x \right)=f\left( 12 \right)=1125$