Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng ${400 {m}}$, dài ${800 {m}}$

Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng ${400 {m}}$, dài ${800 {m}}$. Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm ${A}$, chạy đến điểm ${X}$ và bơi từ điểm ${X}$ đến điểm ${C}$.

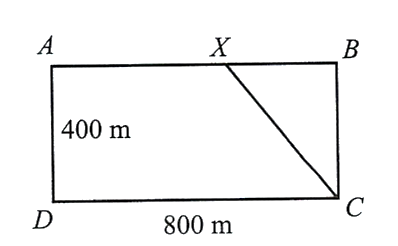
Hỏi nên chọn điểm ${X}$ cách ${A}$ gần bằng bao nhiêu mét để vận động viên đến ${C}$ nhanh nhất ? Biết rằng vận tốc chạy là ${30 {km} / {h}}$, vận tốc bơi là ${6 {km} / {h}}$.
Đáp án: 718

Lời giải: Đặt ${B X=x({km})}$, ta có: ${A X=0,8-x({km})}$;
${X C=\sqrt{(0,4)^2+x^2}=\sqrt{0,16+x^2}({km}) }$
Xét hàm số:
${T(x)=\dfrac{0,8-x}{30}+\dfrac{\sqrt{0,16+x^2}}{6}=\dfrac{1}{30}\left(0,8-x+5 \sqrt{0,16+x^2}\right)(0 \leq x{
Ta có: $T'(x)=\dfrac{1}{30}\left( -1+\dfrac{5x}{\sqrt{0,16+{{x}^{2}}}} \right),T'(x)=0\Rightarrow 5x=\sqrt{0,16+{{x}^{2}}}$.
Bình phương hai vế phương trình ta được ${0,16+x^2=25 x^2 \Leftrightarrow x= \pm \dfrac{\sqrt{6}}{30}}$. Vì ${0{<}x{
Bảng biến thiên của hàm số ${T(x)}$ là:

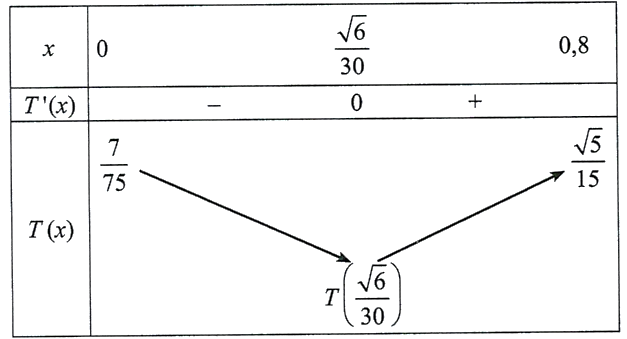
Vậy ${T(x)}$ đạt giá trị nhỏ nhất bằng ${T\left(\dfrac{\sqrt{6}}{30}\right)}$ khi
${A X=0,8-\dfrac{\sqrt{6}}{30} \approx 0,718({km})=718({m}) \text {. } }$