Cho hình vuông $ABCD$ có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với $ABCD$

Cho hình vuông $ABCD$ có cạnh bằng 4, chính giữa có một hình vuông đồng tâm với $ABCD$. Biết rằng bốn tam giác là bốn tam giác cân. Hỏi tổng diện tích của hình vuông ở giữa và bốn tam giác cân nhỏ nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Đáp án: 5,33

Lời giải:

Đặt $AM=x\left( 0{<}x{
$2M{{Q}^{2}}={{\left( 4-2x \right)}^{2}}\Leftrightarrow M{{Q}^{2}}=2{{\left( 2-x \right)}^{2}}\Leftrightarrow MQ=\sqrt{2\left( 2-x \right)}$
Gọi $S$ tổng diện tích của hình vuông ở giữa và bốn tam giác cân nhỏ.
$S=4.\dfrac{M{{Q}^{2}}}{2}+P{{Q}^{2}}=2M{{Q}^{2}}+M{{N}^{2}}={{\left( 4-2x \right)}^{2}}+{{\left( x\sqrt{2} \right)}^{2}}=6{{x}^{2}}-16x+16$ $=0\Leftrightarrow x=\dfrac{4}{3}$
Bảng biến thiên

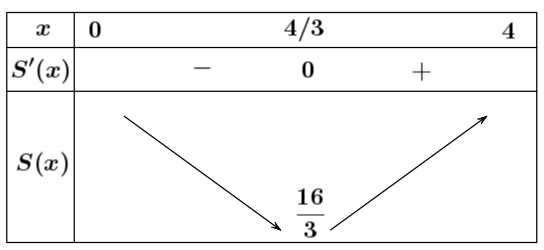
Vậy ${{S}_{\min }}=\dfrac{16}{3}\approx 5,33$