Cho một tấm nhôm hình vuông cạnh $12$ cm

Cho một tấm nhôm hình vuông cạnh $12$ cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x$, rồi gập tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm $x$ để hộp nhận được có thể tích lớn nhất.
Đáp án: 2

Lời giải:

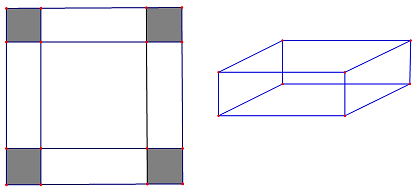
Ta có $h=x\left( \text{cm} \right)$ là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là $12-2x\left( cm \right)$
Ta có $\left\{ \begin{array}{l} x{>}0 \\ 12-2x{>}0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} x{>}0 \\ x{
Thể tích của hình hộp là: $V=x{{\left( 12-2x \right)}^{2}}$.Xét hàm số $y=x{{\left( 12-2x \right)}^{2}},x\in \left( 0;6 \right)$
Ta có ${y}’={{\left( 12-2x \right)}^{2}}-4x\left( 12-2x \right)=\left( 12-2x \right)\left( 12-6x \right)$
Giải phương trình ${y}’=0\Leftrightarrow \left( 12-2x \right)\left( 12-6x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=2 \\ x=6 \end{array} \right.$ ta nhận $x=2$.

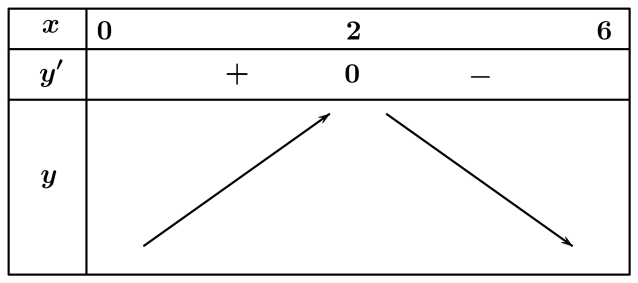
Suy ra giá trị lớn nhất của hàm số là $y\left( 2 \right)=128$. Vậy $x=2$ thì thể tích hộp là lớn nhất.