Nhà xe khoán cho hai tài xế An và Bình mỗi người lần lượt nhận $32$ lít và $72$ lít xăng trong một tháng. Biết rằng trong một ngày tổng số xăng cả hai người sử dụng là 10 lít. Tổng số ngày ít nhất để hai tài xế sử dụng hết số xăng được khoán là bao nhiêu (biết số lít xăng tiêu thụ trong các ngày là như nhau).
Đáp án: 20
Lời giải: Gọi $x$ (lít) $\left( 0{<}x{
Khi đó: $10-x$ (lít) là số xăng Bình sử dụng trong $1$ ngày.
Suy ra $f\left( x \right)=\dfrac{32}{x}+\dfrac{72}{10-x},x\in \left( 0;10 \right)$ là tổng số ngày An và Bình sử dụng hết số xăng được khoán.
Ta có: ${{f}^{‘}}\left( x \right)=-\dfrac{32}{{{x}^{2}}}+\dfrac{72}{{{\left( 10-x \right)}^{2}}}$. Cho ${{f}^{‘}}\left( x \right)=0$ $\Leftrightarrow -\dfrac{32}{{{x}^{2}}}+\dfrac{72}{{{\left( 10-x \right)}^{2}}}=0$ $\Leftrightarrow \left[ \begin{array}{l} x=4 \\ x=-20\notin \left( 0;10 \right) \end{array} \right.$
Bảng biến thiên của hàm số $f\left( x \right)=\dfrac{32}{x}+\dfrac{72}{10-x},x\in \left( 0;10 \right)$
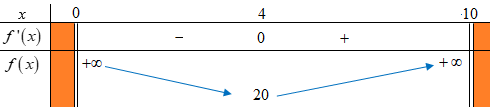
Dựa vào BBT ta có ít nhất $20$ ngày thì An và Bình sử dụng hết lượng xăng được khoán.
Để lại một bình luận