Từ một tấm bìa mỏng hình vuông cạnh 6 ${{dm}}$, bạn Hoa cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, ghép lại tạo thành một khối chóp tứ giác đều

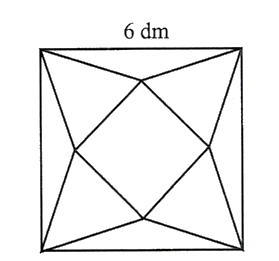
Từ một tấm bìa mỏng hình vuông cạnh 6 ${{dm}}$, bạn Hoa cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, ghép lại tạo thành một khối chóp tứ giác đều. Thể tích của khối chóp có giá trị lớn nhất bằng bao nhiêu decimét khối ?

Đáp án: 7,3

Lời giải: Gọi cạnh đáy của hình chóp tứ giác đều là ${x({dm})}$ với ${0{<}x{

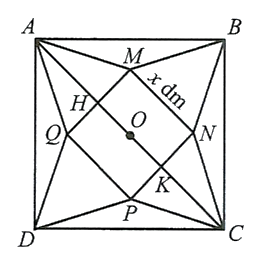
Ta có:
${A H=\dfrac{A C-H K}{2}=3 \sqrt{2}-\dfrac{x}{2} . }$
Đường cao của hình chóp tứ giác đều là:
${h=\sqrt{A H^2-O H^2}=\sqrt{\left(3 \sqrt{2}-\dfrac{x}{2}\right)^2-\left(\dfrac{x}{2}\right)^2}=\sqrt{18-3 \sqrt{2} x}}$.
Thể tích khối chóp là: ${V=\dfrac{1}{3} h x^2=\dfrac{1}{3} x^2 \sqrt{18-3 \sqrt{2} x}=\dfrac{1}{3} \sqrt{x^4(18-3 \sqrt{2} x)}}$.
Để tìm giá trị lớn nhất của ${V}$ ta đi tìm giá trị lớn nhất của hàm số
$f(x)={{x}^{4}}(18-3\sqrt{2}x)\text{, }0{<}x{
Ta có: ${f^{\prime}(x)=x^3(-15 \sqrt{2} x+72), f^{\prime}(x)=0}$ khi ${x=0}$ hoặc ${x=\dfrac{12 \sqrt{2}}{5}}$.
Bảng biến thiên của ${f(x)}$ như sau:

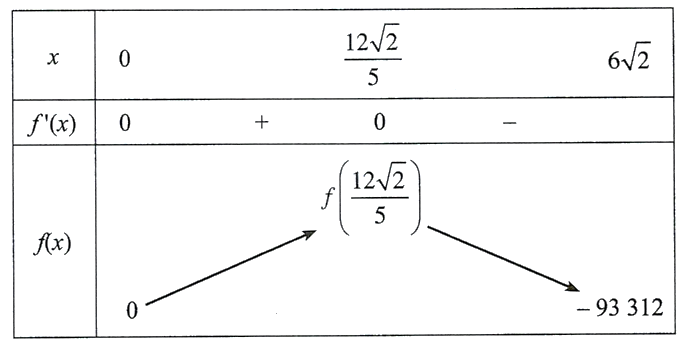
Từ bảng biến thiên ta có ${\max _{(0 ; 6 \sqrt{2})} f\left(\dfrac{12 \sqrt{2}}{5}\right) \approx 477,75}$ tại ${x=\dfrac{12 \sqrt{2}}{5}}$.
Vậy thể tích của khối chóp có giá trị lớn nhất bằng:
${V_{\max }=\dfrac{1}{3} \sqrt{\left(\dfrac{12 \sqrt{2}}{5}\right)^4\left(18-3 \sqrt{2} \cdot \dfrac{12 \sqrt{2}}{5}\right)} \approx 7,3\left({dm}^3\right) . }$