Cho một tấm nhôm hình vuông cạnh $12\text{ cm}$, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( \text{cm} \right)$, rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ)

Cho một tấm nhôm hình vuông cạnh $12\text{ cm}$, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( \text{cm} \right)$, rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).

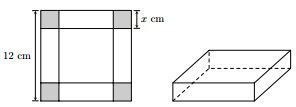
Giá trị của $x$ bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất (làm tròn kết quả đến hàng đơn vị)?
Đáp án: 2

Lời giải: Ta thấy độ dài $x\left( \text{cm} \right)$ của cạnh hình vuông bị cắt phải thoải mãn điều kiện $0{<}x{
Khi đó, thể tích của khối chóp là
$V\left( x \right)=x{{\left( 12-2x \right)}^{2}}=4\left( {{x}^{3}}-12{{x}^{2}}+36x \right),\left( 0{<}x{
Ta có $V’\left( x \right)=4\left( 3{{x}^{2}}-24x+36 \right).$
Phương trình $V’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-24x+36=0\Leftrightarrow \left[ \begin{matrix} x=2 \\ x=6 \\ \end{matrix} \right.$
Bảng biến thiên của hàm số $V\left( x \right)$ như sau:
Từ bảng biến thiên, suy ra $\lim\limits_{\left( 0;6 \right)}V\left( x \right)=V\left( 2 \right)=128\left( c{{m}^{3}} \right).$
Vậy để khối hợp tạo thành có thể tích lớn nhất thì $x=2\text{ cm}\text{.}$