Một công ty bất động sản có $50$ căn hộ cho thuê

Một công ty bất động sản có $50$ căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá $x$ triệu đồng mỗi tháng thì lợi nhuận của công ty sẽ được biểu diễn bởi hàm số $F\left( x \right)=-\dfrac{{{x}^{2}}}{50.000}+90x$ (đồng). Vậy công ty cần cho thuê căn hộ với giá bao nhiêu để lợi nhuận của công ty cao nhất?
Đáp án: 2,25

Lời giải: $F\left( x \right)=-\dfrac{{{x}^{2}}}{50.000}+90x$.
${F}’\left( x \right)=-\dfrac{1}{25.000}x+90$
${F}’\left( x \right)=0\Leftrightarrow -\dfrac{1}{25.000}x+90=0\Leftrightarrow x=2.250.000$
Bảng biến thiên:

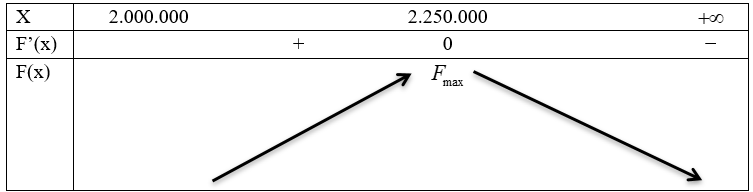
Suy ra $F\left( x \right)$ đạt giá trị lớn nhất khi $x=2.250.000$
Vậy công ty phải cho thuê với giá $2.250.000$ đồng hay 2,25 triệu đồng mỗi căn hộ thì được có lợi nhuận cao nhất.