Hai thành phố A và B cách nhau một con sông

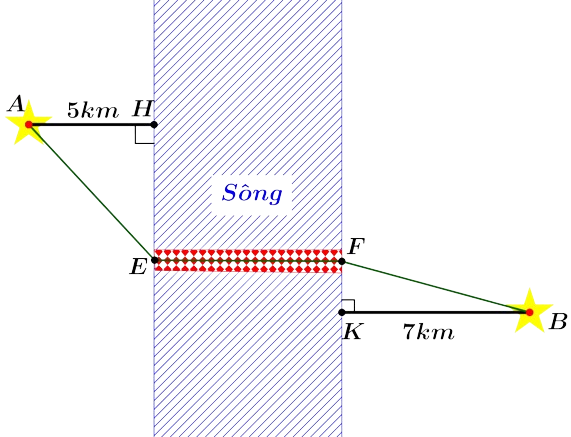
Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu EF bắc qua sông biết rằng thành phố A cách con sông một khoảng là 5km và thành phố B cách con sông một khoảng là 7km, biết $HE+KF=24$ km và độ dài EF không đổi. Hỏi xây cây cầu cách thành phố B là bao nhiêu để đường đi từ thành phố A đến thành phố B là ngắn nhất ?

Đáp án: 16

Lời giải: Đặt $HE={{x}_{{}}}v{{\grave{a}}_{{}}}FK=y$, với $x,y{>}0$
Ta có: $HE+KF=24\Rightarrow x+y=24$
$\left\{ \begin{array}{l} AE=\sqrt{25+{{x}^{2}}} \\ BF=\sqrt{49+{{y}^{2}}}=\sqrt{49+{{\left( 24-x \right)}^{2}}} \end{array} \right.$
Nhận định $AB$ ngắn nhất khi $AE+BF$ nhỏ nhất.
Xét hàm số $f\left( x \right)=\sqrt{{{x}^{2}}+25}+\sqrt{{{\left( 24-x \right)}^{2}}+49}$
${f}’\left( x \right)=\dfrac{x}{\sqrt{{{x}^{2}}+25}}+\dfrac{x-24}{\sqrt{{{x}^{2}}-48x+625}},\forall x\in \left( 0;24 \right)$.
Cho ${f}’\left( x \right)=0\Rightarrow x=10$
Bảng biến thiên

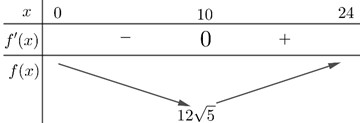
Vậy GTNN của $f(x)$ bằng $7\sqrt{5}$ tại $x=10\Rightarrow BF=7\sqrt{5}\approx 16\text{km}$.