Trong cuộc thi hai môn phối hợp gồm chèo thuyền và chạy xe đạp

Trong cuộc thi hai môn phối hợp gồm chèo thuyền và chạy xe đạp. Các vận động viên sẽ chèo thuyền từ điểm xuất phát $A$ cách bờ $BC$ một khoảng bằng 1km, sau đó đến bờ tại một vị trí $D$ bất kì rồi tiếp tục đạp xe về đích $C$ (tham khảo hình minh họa).

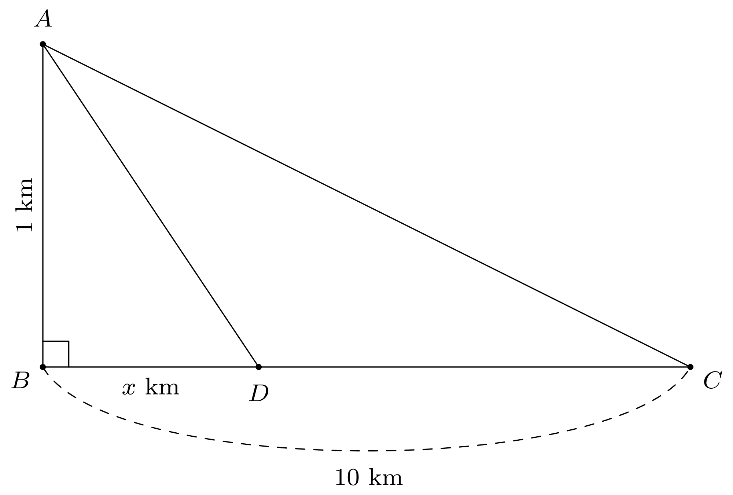
Biết rằng quãng đường trên bờ $BC=10$km và vận tốc trung bình chèo thuyền của vận động viên Phạm Thị Bình là 9km/h và vận tốc trung bình đạp xe trên bờ là 18km/h.
Hỏi Phạm Thị Bình nên chèo thuyền về bờ tại vị trí $D$ cách đích $C$ một khoảng bằng bao nhiêu để tổng thời gian về đích là ngắn nhất (kết quả làm tròn đến hàng phần mười)?
Đáp án: 9,42

Lời giải: Giả sử $BD=x\Rightarrow \left\{\begin{array}{l} DC=10-x\\ AD=\sqrt{x^2+1}\end{array}\right.$, $(0\le x\le 10)$.
Tổng thời gian để vận động viên về đích là $t=\dfrac{\sqrt{x^2+1}}{9}+\dfrac{10-x}{18}$.
Xét hàm số $f(x)=\dfrac{\sqrt{x^2+1}}{9}+\dfrac{10-x}{18}$ trên $[0;10]$.
Ta có $f^{\prime}(x)=\dfrac{x}{9\sqrt{x^2+1}}-\dfrac{1}{18}$.
Phương trình $f^{\prime}(x)=0$ tương đương
\begin{align*}
\sqrt{x^2+1}=2x\Leftrightarrow
\left\{\begin{array}{l} x \ge 0 \\ x^2+1=4x^2\end{array}\right.
\Leftrightarrow \left\{\begin{array}{l} x \ge 0 \\ 3x^2-1=0\end{array}\right.
\Leftrightarrow x=\frac{\sqrt{3}}{3} \in [0;10].
\end{align*}
Bảng biến thiên của hàm số $f(x)$ trên $[0;10]$ như sau:

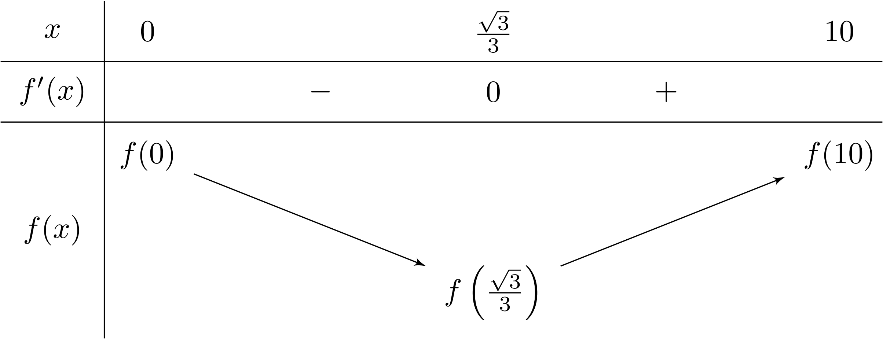
Vậy vận động viên nên vào bờ tại vị trí $D$ cách đích $C$ một khoảng là
$DC = BC – x=10-\frac{\sqrt{3}}{3}\approx 9,42$ km để tổng thời gian về đích là ngắn nhất.