Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng $108 \mathrm{cm}^2$ như Hình 1

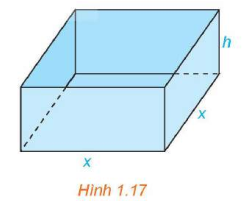
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng $108 \mathrm{cm}^2$ như Hình 1.17. Tìm chiều cao của chiếc hộp sao cho thể tích của chiếc hộp là lớn nhất.

Đáp án: 3

Lời giải: Hình hộp trên có độ dài cạnh đáy là x ( $\mathrm{cm}, x{>}0)$ và chiều cao là h ( $\mathrm{cm}, h{>}0)$
Diện tích bề mặt của hình hộp là $108 \mathrm{cm}^2$ nên $x^2+4 x h=108 \Rightarrow h=\dfrac{108-x^2}{4 x}(\mathrm{cm})$ (điều kiện $0{<}x{
Thể tích của hình hộp là: $V=x^2 . h=x^2 \cdot \dfrac{108-x^2}{4 x}=\dfrac{108 x-x^3}{4}\left(\mathrm{cm}^3\right)$. Bài toán trở thành tìm giá trị lớn nhất của hàm số $0{<}x{
Ta có: ${V}’=\dfrac{-3{{x}^{2}}+108}{4},{V}’=0\Leftrightarrow x=6$ (do $0{<}x{
Lập bảng biến thiên của hàm số

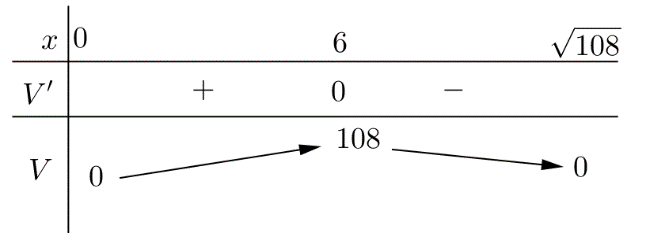
Do đó, thể tích của chiếc hộp là lớn nhất khi độ dài cạnh đáy $x=6 \mathrm{cm}$
Khi đó, chiều cao của chiếc hộp là: $\dfrac{108-6^2}{4.6}=3(\mathrm{cm})$.