Một tấm bạt hình vuông cạnh $20m$ như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt rồi gập và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tháp đèn trang trí (tháp dạng hình chóp tứ giác đều) để tránh hư hại tháp khi trời mưa.
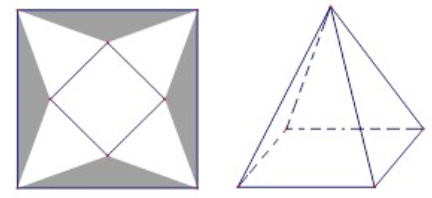
Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi phần diện tích tấm bạt bị cắt là bao nhiêu để đảm bảo yêu cầu trên.
Đáp án: 80
Lời giải:
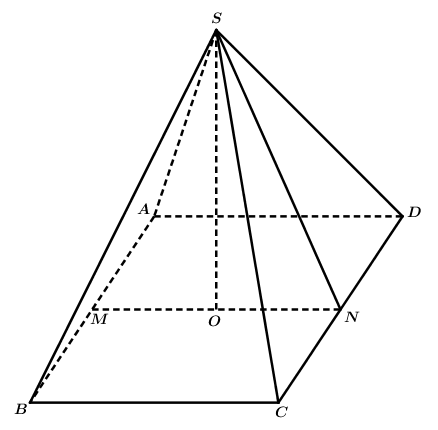
Gọi cạnh đáy hình vuông của tháp là $x\left( m \right)$.
Độ dài đường chéo tấm bạt bằng $20\sqrt{2}\left( m \right)$.
Gọi hình chóp tứ giác đều là $S.ABCD$, Gọi $M,N$ lần lượt là trung điểm $AB,CD$.
Khi đó $MN=x\left( m \right)$, $SN=\dfrac{20\sqrt{2}-x}{2}\left( m \right)$ với $0{<}x{
Gọi $O$ là tâm của hình vuông, ta có
$SO=\sqrt{S{{N}^{2}}-O{{N}^{2}}}=\sqrt{{{\left( \dfrac{20\sqrt{2}-x}{2} \right)}^{2}}-{{\left( \dfrac{x}{2} \right)}^{2}}}=\dfrac{1}{2}\sqrt{800-40\sqrt{2}x}$.
Thể tích khối chóp $V=\dfrac{1}{3}{{S}_{ABCD}}.SO=\dfrac{1}{6}{{x}^{2}}\sqrt{800-40\sqrt{2}x}$.
Ta có $V’=\dfrac{20x\left( 80-5\sqrt{2}x \right)}{6\sqrt{800-40\sqrt{2}x}}$
$\Rightarrow V’=0\Leftrightarrow x=8\sqrt{2}$ với $0{<}x{
Xét bảng biến thiên:
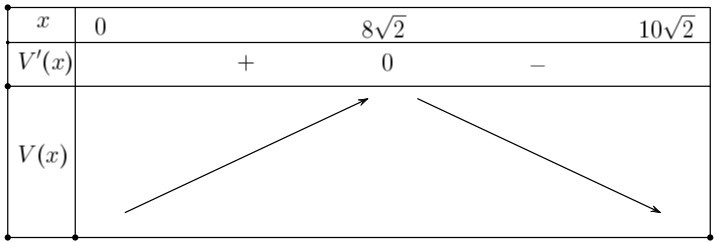
Vậy khi $x=8\sqrt{2}$ thì thể tích khối chóp lớn nhất $V=\dfrac{256\sqrt{10}}{3}\left( {{m}^{3}} \right)$.
Diện tích phần bị cắt của tấm bạt:
$S={{S}_{hv}}-{{S}_{ABCD}}-4.{{S}_{\Delta SAB}}={{20}^{2}}-{{\left( 8\sqrt{2} \right)}^{2}}-4.\dfrac{1}{2}.\dfrac{20\sqrt{2}-8\sqrt{2}}{2}.8\sqrt{2}=80\left( {{m}^{2}} \right)$.
