Nhằm tăng tính cạnh tranh trên thị trường vào dịp Tết Nguyên Đán, công ty nước giải khát K dự định bổ sung một số sản phẩm mới trong đó có mẫu lon nước giải khát dung tích $500ml$ (mililit) dạng hình trụ

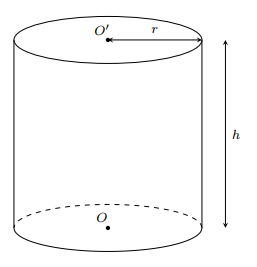
Nhằm tăng tính cạnh tranh trên thị trường vào dịp Tết Nguyên Đán, công ty nước giải khát K dự định bổ sung một số sản phẩm mới trong đó có mẫu lon nước giải khát dung tích $500ml$ (mililit) dạng hình trụ. Để giảm chi phí logistic các nhà thiết kế cần thiết kế mẫu lon nước này có bán kính đường tròn đáy bằng bao nhiêu centimet để tiết kiệm vật liệu nhất? (Kết quả làm tròn đến hàng phần trăm). Biết rằng thể tích của khối trụ và diện tích xung quanh của hình trụ lần lượt là $\pi {{r}^{2}}h$ và $2\pi rh$.

Đáp án: 4,3

Lời giải: Ta có: $\pi {{r}^{2}}h=500\Rightarrow h=\dfrac{500}{\pi {{r}^{2}}}$.
Để tiết kiệm vật liệu nhất thì diện tích toàn phần của lon nước hình trụ là nhỏ nhất
Diện tích toàn phần của hình trụ là: $S=2\pi rh+2\pi {{r}^{2}}=2\pi r.\dfrac{500}{\pi {{r}^{2}}}+2\pi {{r}^{2}}=\dfrac{1000}{r}+2\pi {{r}^{2}}=f\left( r \right)$
$f’\left( r \right)=\dfrac{-1000}{{{r}^{2}}}+4\pi r\Rightarrow f’\left( r \right)=0\Leftrightarrow r=\dfrac{10}{\sqrt[3]{4\pi }}$
Ta có bảng biến thiên

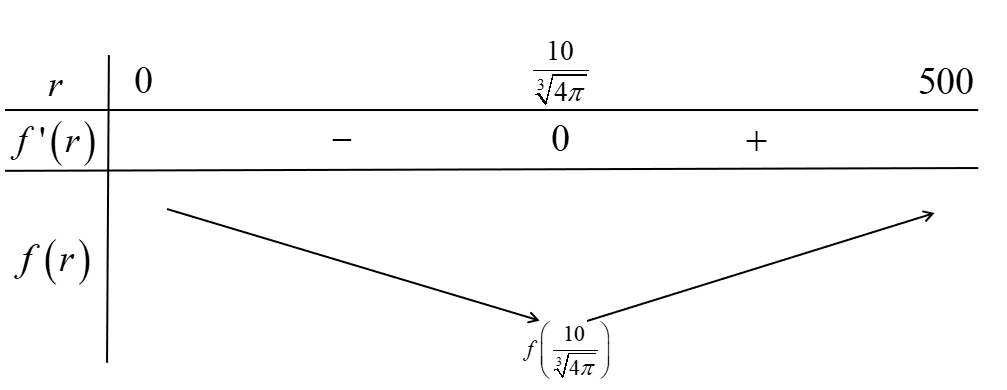
Từ bảng biến thiên suy ra để tiết kiệm nguyên vật liệu nhất thì bán kính đường tròn đáy là $r=\dfrac{10}{\sqrt[3]{4\pi }}\simeq 4,30$