Trong 30 ngày đầu tiên sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân thứ nhất đến ngày thứ $t$ được xác định theo hàm số $f\left( t \right)=114{{t}^{2}}-2{{t}^{3}};t\le 30,t\in \mathbb{N}*$ và quy ước tốc độ truyền bệnh là hàm ${f}’\left( t \right)$ (người/ngày). Hỏi tốc độ truyền bệnh tăng dần đến ngày thứ bao nhiêu thì bắt đầu giảm dần?
Đáp án: 15
Lời giải: Ta có hàm tốc độ truyền bệnh là $g\left( t \right)={f}’\left( t \right)=228t-6{{t}^{2}};{g}’\left( t \right)=228-12t$.
${g}’\left( t \right)=0\Leftrightarrow t=19$.
Ta có bảng biến thiên
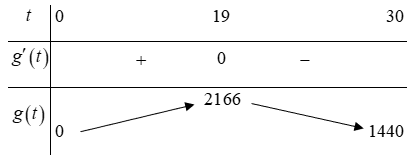
Dựa vào bảng biến thiên ta thấy tốc độ truyền bệnh tăng dần đến ngày thứ 15 thì bắt đầu giảm dần.
