Hàng ngày mực nước của hồ thủy điện ở
miền Trung lên và xuống theo lượng nước mưa, và các suối nước đổ về hồ

Hàng ngày mực nước của hồ thủy điện ở
miền Trung lên và xuống theo lượng nước mưa, và các suối nước đổ về hồ. Từ lúc $6h$ sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức $h(t) = \frac{t^{3}}{3} – \frac{7 t^{2}}{3} – \frac{44 t}{3}$. Biết rằng phải thông báo cho các hộ dân phải di dời trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời vào lúc mấy giờ? Biết rằng mực nước trong hồ phải lên cao nhất mới xả nước.
Đáp án: 11

Lời giải: Ta có $h'(t)=t^{2} – \frac{14 t}{3} – \frac{44}{3}$; $h'(t)=0\Leftrightarrow t^{2} – \frac{14 t}{3} – \frac{44}{3}=0\Leftrightarrow \left[\begin{array}{l} t=-4\text{ (loại)}\\ t=11\text{ (nhận).}\end{array}\right.$
Bảng biến thiên

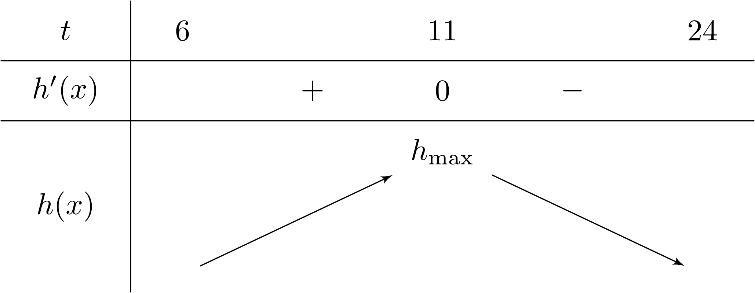
Vậy để mực nước lên cao nhất thì phải mất $11$ giờ.
Vậy phải thông báo cho dân di dời vào $12$ giờ chiều cùng ngày.