Hai xe khởi hành cùng lúc trên $2$ con đường vuông góc với nhau tại vị trí $O$

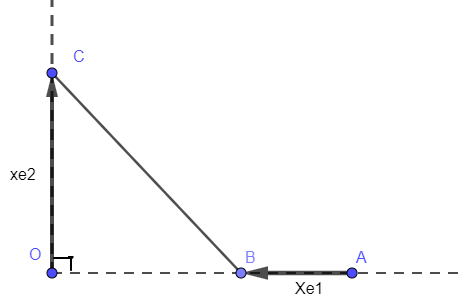
Hai xe khởi hành cùng lúc trên $2$ con đường vuông góc với nhau tại vị trí $O$. Xe thứ nhất xuất phát từ vị trí $A$ trên đường thứ nhất chạy về vị trí $O$, xe thứ 2 xuất phát từ $O$ chạy trên đường thứ hai.Biết rằng $A$ cách $O$ một khoảng bằng $80$ km, vận tốc của xe thứ hai gấp đôi vận tốc của xe thứ nhất. Khi xe thứ nhất đến vị trị $B$ thì xe thứ hai đến vị trí $C$ và khoảng cách từ $B$ đến $C$ là nhỏ nhất. Hỏi khoảng cách nhỏ nhất đó bằng bao nhiêu km?

Đáp án: 71,6

Lời giải: $AB=x$ km? $OC=2x$ km và $OB=\left( 80-x \right)$ km
ĐK: $0{<}x{
$\begin{array}{l} BC=\sqrt{{{(2x)}^{2}}+{{(80-x)}^{2}}}=\sqrt{5{{x}^{2}}-160x+6400}=\sqrt{g(x)} \\ {g}'(x)=10x-160=0\Leftrightarrow x=16\Rightarrow {{g}_{\min }}=g(16)=5120 \\ \Rightarrow B{{C}_{\min }}=\sqrt{5120}=32\sqrt{5}\approx 71,6 \end{array}$.