Doanh số bán hệ thống âm thanh mới đưa ra thị trường trong một khoảng thời gian dự kiến sẽ tuân theo đường cong logistic $R\left( x \right)=\dfrac{5000{{\text{e}}^{x}}}{{{e}^{x}}+5},x\ge 0$, trong đó thời gian $x$ tính bằng năm

Doanh số bán hệ thống âm thanh mới đưa ra thị trường trong một khoảng thời gian dự kiến sẽ tuân theo đường cong logistic $R\left( x \right)=\dfrac{5000{{\text{e}}^{x}}}{{{e}^{x}}+5},x\ge 0$, trong đó thời gian $x$ tính bằng năm. Biết tốc độ bán hàng là $R’\left( x \right)$ đạt tối đa vào gần thời điểm năm nào nhất?
Đáp án: 2

Lời giải: Hàm số biểu thị tốc độ bán hàng là ${R}’\left( x \right)=\dfrac{25000{{\text{e}}^{x}}}{{{\left( {{e}^{x}}+5 \right)}^{2}}}$.
$\Rightarrow {{R}’}’\left( x \right)=\dfrac{25000{{\text{e}}^{x}}\left( 5-{{e}^{x}} \right)}{{{\left( {{e}^{x}}+5 \right)}^{3}}}$.
${{R}’}’\left( x \right)=0\Leftrightarrow x=\ln 5\approx 1,61$
Bảng biến thiên

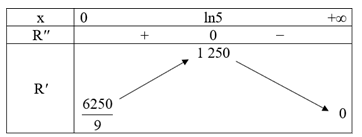
Suy ra tốc độ bán đạt tối đa vào gần thời điểm năm thứ hai.