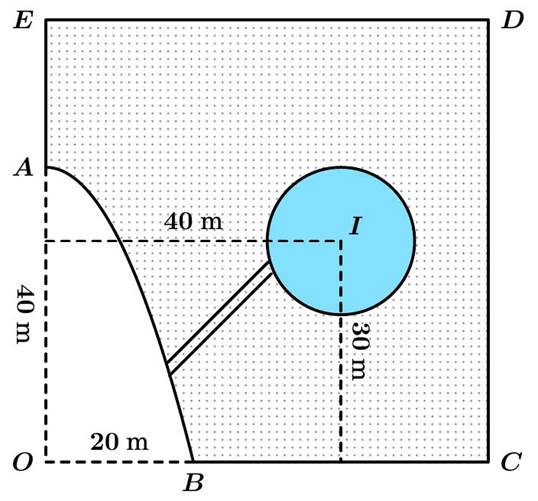
- Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:
– Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O;
– Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ;
– Độ dài đoạn OA và OB lần lượt là 40m và 20m;
– Tâm I của mảnh vườn cách đường thẳng AE và BC lần lượt là 40m và 30m.

Lời giải
Chọn hệ trục tọa độ Đề các vuông góc như sau: Gốc O, chiều dương trục hoành là tia OC, chiều dương trục tung là tia OE, đơn vị hai trục là đơn vị độ dài (1m).
Khi đó ta có phương trình Parabol là: $y=-\frac{1}{10}{{x}^{2}}+40$ và phương trình đường tròn là: ${{\left( x-40 \right)}^{2}}+{{\left( y-30 \right)}^{2}}=100$
Đường tròn có tâm $I\left( 40;30 \right)$ và bán kính $R=10$
Lấy điểm $M\left( t;-\frac{1}{10}{{t}^{2}}+40 \right)$ (với $0\le t\le 20$) nằm trên parabol thì khoảng cách ngắn nhất từ M đến đường tròn là $IM-R=\sqrt{\frac{1}{100}{{t}^{4}}-{{t}^{2}}-80t+1700}-10$
Tìm GTNN của hàm số $f(t)=\frac{1}{100}{{t}^{4}}-{{t}^{2}}-80t+1700$ trên đoạn $\left[ 0;20 \right]$ ta được $\underset{\left[ 0;20 \right]}{\mathop{\min }}\,f(t)\approx 768,0877$
Do đó độ dài ngắn nhất $l\approx \sqrt{768,0877}-10\approx 17,7$.
