DẠNG TOÁN 43 THỂ TÍCH KHỐI ĐA DIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Cho khối chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh\(a\), tâm \(O\), \(SA\) vuông góc với với mặt phẳng \(\left( {ABCD} \right)\). Góc giữa đường thẳng […]
Trắc nghiệm Khối đa diện
Cho hình chóp tam giác \(S.ABC\) có \(SA = 2a\)và \(SA\) tạo với mặt phẳng \(\left( {ABC} \right)\) góc\(30^\circ \). Tam giác \(ABC\) vuông cân tại \(B\), \(G\) là trọng tâm tam giác \(ABC\). Hai mặt phẳng \(\left( {SGB} \right)\) và \(\left( {SGC} \right)\)cùng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp \(S.ABC\) theo \(a\).
DẠNG TOÁN 43 THỂ TÍCH KHỐI ĐA DIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Cho hình chóp tam giác \(S.ABC\) có \(SA = 2a\)và \(SA\) tạo với mặt phẳng \(\left( {ABC} \right)\) góc\(30^\circ \). Tam giác \(ABC\) vuông cân tại […]
Cho tứ diện \(OABC\) có ba cạnh \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau, \(OA = \frac{{a\sqrt 2 }}{2}\), \(OB = OC = a\). Gọi \(H\) là hình chiếu của điểm \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Tính thể tích khối tứ diện \(OABH\).
DẠNG TOÁN 43 THỂ TÍCH KHỐI ĐA DIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Cho tứ diện \(OABC\) có ba cạnh \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau, \(OA = \frac{{a\sqrt 2 }}{2}\), \(OB = OC = a\). […]
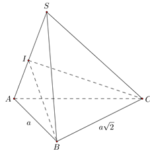
Cho hình chóp \(S.ABC\) có \(AB = a\), \(AC = a\sqrt 3 \), \(SB > 2a\) và \(\widehat {ABC} = \widehat {BAS} = \widehat {BCS} = 90^\circ \), sin của góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAC} \right)\) bằng \(\frac{{\sqrt {11} }}{{11}}\). Tính thể tích khối chóp \(S.ABC\).
DẠNG TOÁN 43 THỂ TÍCH KHỐI ĐA DIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Cho hình chóp \(S.ABC\) có \(AB = a\), \(AC = a\sqrt 3 \), \(SB > 2a\) và \(\widehat {ABC} = \widehat {BAS} = \widehat {BCS} = […]
Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình vuông có cạnh \(a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, mặt bên \(\left( {SCD} \right)\) hợp với mặt phẳng đáy một góc \(60^\circ \). Tính thể tích hình chóp \(S.ABCD\).
DẠNG TOÁN 43 THỂ TÍCH KHỐI ĐA DIỆN – phát triển theo đề tham khảo Toán 2021 Theo đề tham khảo Toán 2021 của Bộ GD&ĐT ĐỀ BÀI: Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình vuông có cạnh \(a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, mặt bên \(\left( {SCD} \right)\) […]
Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều. Hình chiếu vuông góc của \(A’\) trên mặt phẳng \((ABC)\) là trung điểm \(BC\). Mặt phẳng \((P)\) vuông góc với các cạnh bên và cắt các cạnh bên của hình lăng trụ lần lượt tại \(D,E,F\). Biết mặt phẳng \((ABB’A’)\) vuông góc với mặt phẳng \((ACC’A’)\) và chu vi tam giác \(DEF\) bằng 4, thể tích của khối lăng trụ \(ABC.A’B’C’\) bằng
Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều. Hình chiếu vuông góc của \(A’\) trên mặt phẳng \((ABC)\) là trung điểm \(BC\). Mặt phẳng \((P)\) vuông góc với các cạnh bên và cắt các cạnh bên của hình lăng trụ lần lượt tại \(D,E,F\). Biết mặt phẳng \((ABB’A’)\) vuông góc với mặt […]
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng và O là tâm của đáy. Gọi M, N, P và Q lần lượt là hình chiếu vuông góc của O trên các mặt phẳng (SAB), (SBC), (SCD) và (SDA). Thể tích của khối chóp O.MNPQ
Câu hỏi: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\frac{{\sqrt 3 a}}{2}\) và O là tâm của đáy. Gọi M, N, P và Q lần lượt là hình chiếu vuông góc của O trên các mặt phẳng (SAB), (SBC), (SCD) và (SDA). Thể tích của khối chóp O.MNPQ bằng A. \(\frac{{{a^3}}}{{48}}\) B. […]
Câu 49: (MH Toan 2020) Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\), \(\widehat {SBA} = \widehat {SCA} = 90^\circ \), góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) bằng \(60^\circ \). Thể tích của khối chóp đã cho bằng
Câu 49: (MH Toan 2020) Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\), \(\widehat {SBA} = \widehat {SCA} = 90^\circ \), góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) bằng \(60^\circ \). Thể tích của khối chóp đã cho bằng A. \({a^3}\). B. \(\frac{{{a^3}}}{3}\). C. \(\frac{{{a^3}}}{2}\). […]
Đề: Một đứa trẻ dán 42 hình lập phương cạnh 1cm lại với nhau vừa đủ xung quanh mặt của một khối hộp chữ nhật tạo thành một khối hộp mới. Nếu chu vi đáy là 18cm thì chiều cao của khối hình hộp lúc này là bao nhiêu?
Câu hỏi: Một đứa trẻ dán 42 hình lập phương cạnh 1cm lại với nhau vừa đủ xung quanh mặt của một khối hộp chữ nhật tạo thành một khối hộp mới. Nếu chu vi đáy là 18cm thì chiều cao của khối hình hộp lúc này là bao nhiêu? A. 6cm B. 3cm C. […]
Đề: Cho hình chóp đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Khi đó thể tích hình chóp bằng:
Câu hỏi: Cho hình chóp đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Khi đó thể tích hình chóp bằng: A. \(\frac{{{x^3}\sqrt 3 }}{6}.\) B. \(\frac{{{x^3}\sqrt 3 }}{2}.\) C. \(\frac{{{x^3}\sqrt 3 }}{{12}}.\) D. \(\frac{{{x^3}\sqrt 3 }}{3}.\) Hãy chọn trả lời đúng trước khi xem đáp án và lời […]