Câu 49: (MH Toan 2020) Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\), \(\widehat {SBA} = \widehat {SCA} = 90^\circ \), góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) bằng \(60^\circ \). Thể tích của khối chóp đã cho bằng

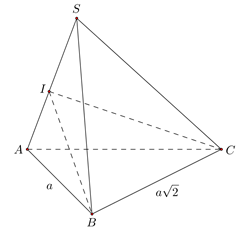
Câu 49: (MH Toan 2020) Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\), \(\widehat {SBA} = \widehat {SCA} = 90^\circ \), góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) bằng \(60^\circ \). Thể tích của khối chóp đã cho bằng
A. \({a^3}\).
B. \(\frac{{{a^3}}}{3}\).
C. \(\frac{{{a^3}}}{2}\).
D. \(\frac{{{a^3}}}{6}\).

Lời giải
Cách 1:
Đáp án: D

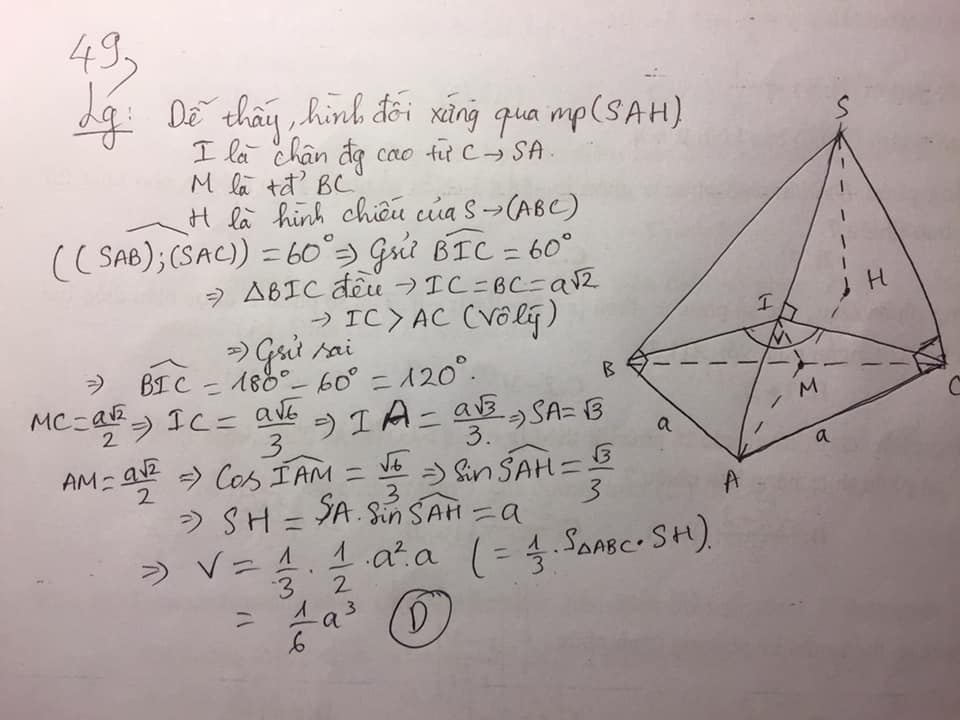
Hai tam giác \[SAB\] và ${SAC}$ bằng nhau chung cạnh huyền ${SA}$.
Kẻ ${BI}$ vuông góc với ${SA}$ suy ra ${CI}$ cũng vuông góc với ${SA}$ và $IB=IC$.
$SA\bot IC$, $SA\bot IB$ $\Rightarrow SA\bot(IBC)$ tại $I$
$V_{S.ABC}=V_{A.IBC}+V_{S.IBC}=\dfrac{1}{3}S_{\Delta IBC}.AI+\dfrac{1}{3}S_{\Delta IBC}.SI=\dfrac{1}{3}S_{\Delta IBC}\left(AI+SI\right)=\dfrac{1}{3}S_{\Delta IBC}.SA$
$\left((SAB),(SAC)\right)=(IB,IC)$ $\Rightarrow(IB,IC)=60\circ$ $\Rightarrow \widehat{BIC}=60\circ$ hoặc $\widehat{BIC}=120\circ$.
Trong tam giác ${IBC}$ đặt $IB=IC=x$ $(x>0)$, ta có
$\cos 120\circ=\dfrac{IB^2+IC^2-BC^2}{2IB.IC}\Rightarrow-\dfrac{1}{2}=\dfrac{2x^2-\left(a\sqrt{2}\right)^2}{2x^2}\Rightarrow x=\dfrac{a\sqrt{6}}{3}\Rightarrow IB=IC=\dfrac{a\sqrt{6}}{3}$
Trong tam giác ${ABI}$ vuông tại $I$ có $AI=\sqrt{AB^2-IB^2}=\sqrt{a^2-\left(\dfrac{a\sqrt{6}}{3}\right)^2}=\dfrac{a\sqrt{3}}{3}$
Trong tam giác ${SAB}$ vuông tại $B$ đường cao ${BI}$ có $AB^2=IA.SA\Rightarrow SA=\dfrac{AB^2}{IA}=\dfrac{a^2}{\dfrac{a\sqrt{3}}{3}}=a\sqrt{3}$
Vậy $V_{S.ABC}=\dfrac{1}{3}.S_{\Delta IBC}.SA=\dfrac{1}{3}.\dfrac{1}{2}.IB.IC.SA.\sin \widehat{BIC}=\dfrac{1}{6}\left(\dfrac{a\sqrt{6}}{3}\right)^3a\sqrt{3}\sin120\circ=\dfrac{a^3}{6}$
===========
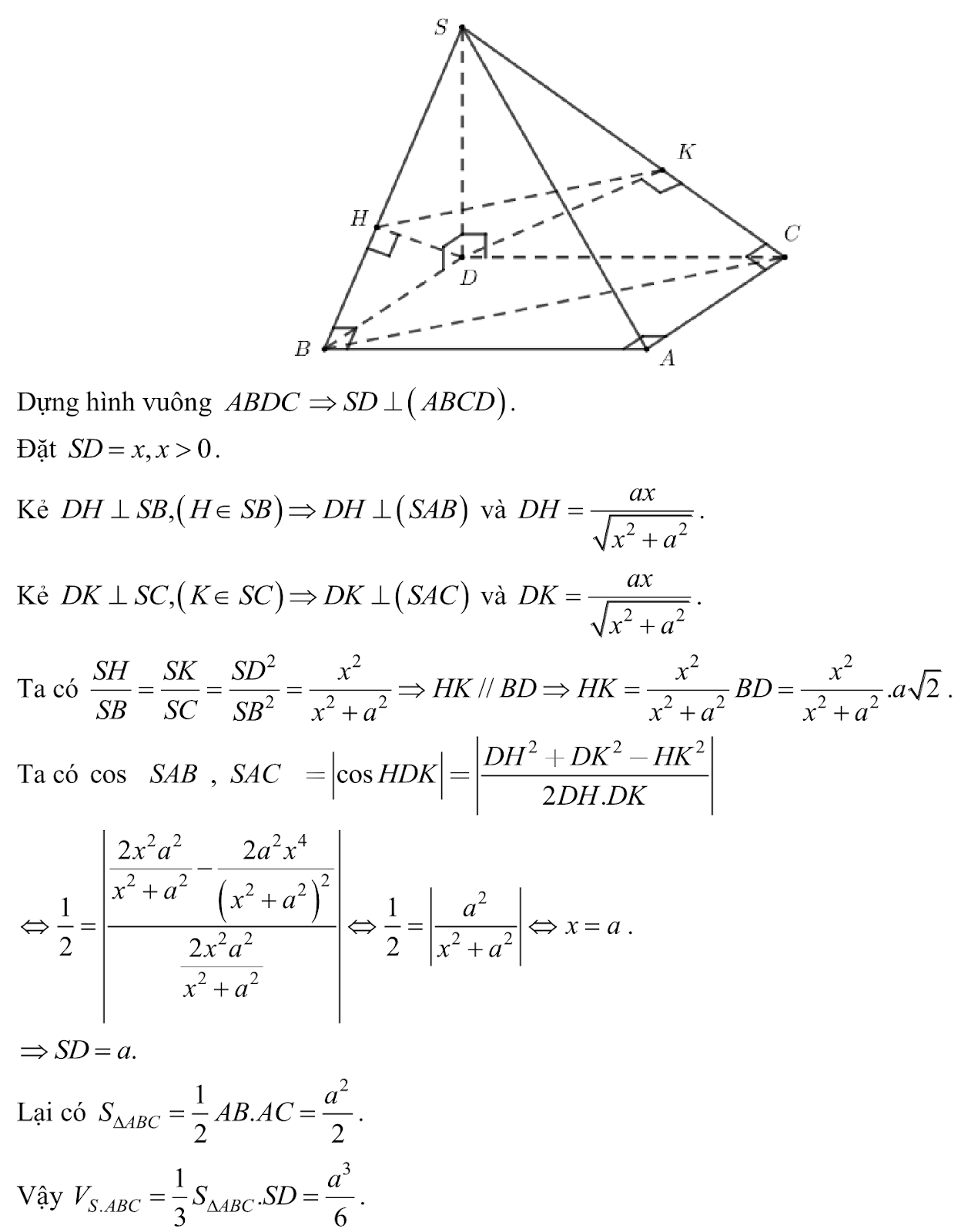
Cách 2:

Cách 3

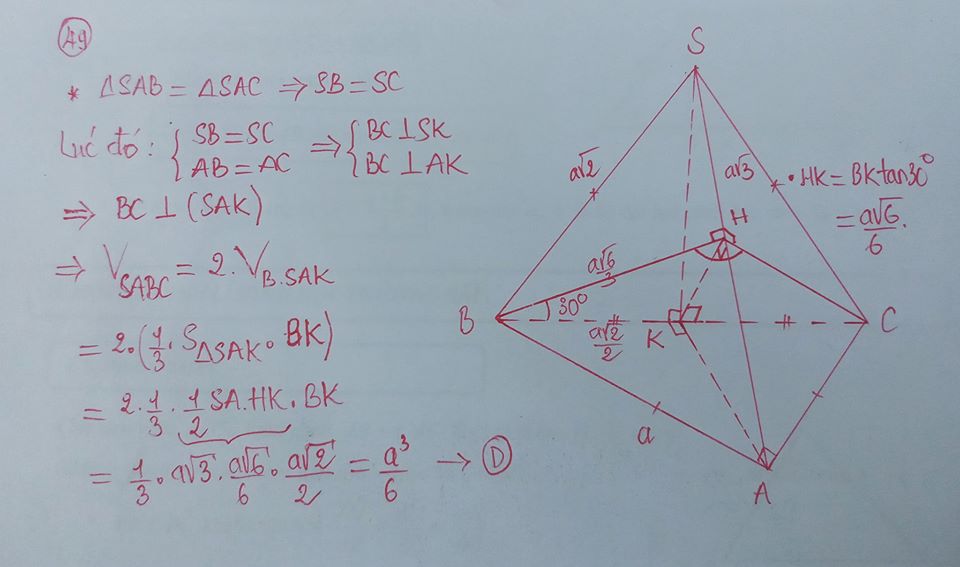
cách 4:

Cách 5:Minh Hoàng (tọa độ hóa).
Không mất tính tổng quát, ta có thể giả sử a=1.

Cách 6: