Tìm tham số m để hàm số đơn điệu trên một miền

Tìm tham số m để hàm số đơn điệu trên một miền

Ta xét dạng toán tìm điều kiện của tham số $m$ để hàm số đơn điệu trên $R$ hoặc trên khoảng con của $R.$

Lý thuyết:
Cho hàm số $y = f\left( {x,m} \right)$ với $m$ là tham số xác định trên một khoảng $I.$
a. Hàm số đồng biến trên $I$ $ \Leftrightarrow y’ \ge 0, \forall x \in I$ và $y’ = 0$ chỉ xảy ra tại hữu hạn điểm.
b. Hàm số nghịch biến trên $I$ $ \Leftrightarrow y’ \le 0, \forall x \in I$ và $y’ = 0$ chỉ xảy ra tại hữu hạn điểm.
Chú ý: Để xét dấu của $y’$ ta thường sử dụng phương pháp hàm số hay định lý về dấu của tam thức bậc hai như sau:
Cho tam thức bậc hai: $g\left( x \right) = a{x^2} + bx + c, \left( {a \ne 0} \right).$
a. Nếu $\Delta < 0$ thì $g(x)$ luôn cùng dấu với $a.$
b. Nếu $\Delta = 0$ thì $g(x)$ luôn cùng dấu với $a$ (trừ $x = – \frac{b}{{2a}}$).
c. Nếu $\Delta > 0$ thì phương trình $g\left( x \right) = 0$ luôn có hai nghiệm phân biệt, khi đó dấu của $g(x)$ trong khoảng hai nghiệm thì khác dấu với hệ số $a$, ngoài khoảng hai nghiệm thì cùng dấu với hệ số $a.$
Các bước cơ bản để giải bài toán tìm giá trị của tham số để hàm số đơn điệu trên một khoảng xác định:
+ Bước 1: Tìm miền xác định.
+ Bước 2: Tìm đạo hàm.
+ Bước 3: Áp dụng lý thuyết vửa nhắc ở trên.

==============

Ví dụ 1:

Tìm tất cả các giá trị thực của tham số m để hàm số \(y=x^3+3x^2+mx+m\) đồng biến trên \(\mathbb{R}\).

Lời giải:

• Xét hàm số \(y=x^3+3x^2+mx+m\)
  • TXĐ: \(D=\mathbb{R}\)
  • \(y’ = 3{x^2} + 6x + m\)
• Hàm số đồng biến trên \(\mathbb{R}\) khi \(y’ \ge 0,\forall x \in\mathbb{R} \Leftrightarrow \left\{ \begin{array}{l} \Delta ‘ \le 0\\ a = 1 > 0 \end{array} \right. \Leftrightarrow 9 – 3m < 0 \Leftrightarrow m \ge 3\).
• Kết luận: với \(m\geq 3\) thì hàm số đồng biến trên \(\mathbb{R}\).

Ví dụ 2:

Tìm tất cả các giá trị thực của tham số m để hàm số \(y = 2x^3 – 3(2m + 1){x^2} + 6m(m + 1)x + 1\) đồng biến trong khoảng \((2; + \infty )\).

Lời giải:

• Xét hàm số \(y = 2x^3 – 3(2m + 1){x^2} + 6m(m + 1)x + 1\).
  • TXĐ: \(D=\mathbb{R}\)
  • \(y’ = 6{x^2} – 6(2m + 1)x + 6m(m + 1)\)
  • \(\Delta = {(2m + 1)^2} – 4({m^2} + m) = 1 > 0\)
  • \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = m\\ x = m + 1 \end{array} \right.\)
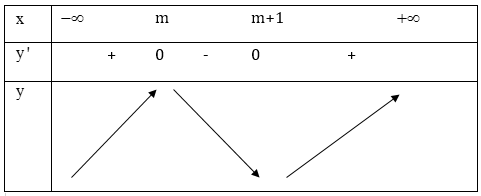
• Do \(m<m+1\) nên ta có bảng biến thiên:

• Hàm số đồng biến trong các khoảng \(( – \infty ;m),\,\,(m + 1; + \infty )\).
• Kết luận: Do đó hàm số đồng biến trong khoảng \((2; + \infty )\) khi \(m + 1 \le 2 \Leftrightarrow m \le 1.\)

Ví dụ 3:  Trong tất cả các giá trị của tham số $m$ để hàm số $y = \frac{1}{3}{x^3} + m{x^2} – mx – m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là?
Phân tích: Đây là hàm bậc ba, ta xét $y’ \ge 0, \forall x \in R$, dấu bằng xảy ra tại hữu hạn điểm để tìm giá trị nhỏ nhất của $m.$
Lời giải: Ta có $y’ = {x^2} + 2mx – m$. Để hàm số đã cho luôn đồng biến trên $R$ thì $\Delta’ \le 0$ với mọi $m$ $ \Leftrightarrow {m^2} + m \le 0$ $ \Leftrightarrow – 1 \le m \le 0$. Vậy giá trị nhỏ nhất của $m$ thỏa mãn là $m = -1$.

Ví dụ 4:  Điều kiện cần và đủ để hàm số $y = \frac{{mx + 5}}{{x + 1}}$ đồng biến trên từng khoảng xác định là?
Phân tích: Hàm số bậc nhất trên bậc nhất có dạng $y = \frac{{ax + b}}{{cx + d}}$ có đạo hàm $y’ = \frac{{ad – bc}}{{{{\left( {cx + d} \right)}^2}}}$ luôn đơn điệu trên từng khoảng xác định (chứ không phải trên tập xác định).
Đồng biến trên từng khoảng xác định khi $ad – bc > 0$, nghịch biến trên từng khoảng xác định khi $ad – bc < 0.$
Lời giải: Ta có $y’ = \frac{{m – 5}}{{{{\left( {x + 1} \right)}^2}}}$. Để hàm số đã cho luôn đồng biến trên từng khoảng xác định thì $m – 5 > 0 \Leftrightarrow m > 5.$

Ví dụ 5:  Cho hàm số $y = \frac{{mx + 2 – 2m}}{{x + m}} (1)$ ($m$ là tham số). Tìm $m$ để hàm số $(1)$ đồng biến trên từng khoảng xác định.
Phân tích: Một bài toán về hàm phân thức bậc nhất trên bậc nhất nhưng có tham số ở mẫu. Nếu bài toán hỏi “Tìm $m$ để hàm số $(1)$ nghịch biến (hoặc đồng biến) trên một khoảng $\left( {a;b} \right)$ nhất định thì bài toán phải thêm điều kiện, tuy nhiên ở đây ta có thể giải đơn giản như sau:
Lời giải: Điều kiện $x \ne – m.$
Ta có $y’ = \frac{{{m^2} + 2m – 2}}{{{{\left( {x + m} \right)}^2}}}$. Để hàm số đã cho đồng biến trên từng khoảng xác định thì:
${m^2} + 2m – 2 > 0$ $ \Leftrightarrow \left[ \begin{array}{l}
m > – 1 + \sqrt 3 \\
m < – 1 – \sqrt 3
\end{array} \right.$
Ví dụ 6:  Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \frac{{x + 2 – 2m}}{{x + m}}$ đồng biến trên $\left( { – 1;2} \right)$.
Phân tích: Hàm số đơn điệu trên khoảng nào thì phải xác định trên khoảng đó. Do vậy ở đây cần có điều kiện cho $ – m \notin \left( { – 1;2} \right)$.
Lời giải: Để hàm số đã cho đồng biến trên $\left( { – 1;2} \right)$ thì $y’ > 0$ với mọi $x \in \left( { – 1;2} \right).$
$ \Leftrightarrow \left\{ \begin{array}{l}
m – \left( {2 – 2m} \right) > 0\\
– m \notin \left( { – 1;2} \right)
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
3m – 2 > 0\\
\left[ \begin{array}{l}
m \ge 1\\
m \le – 2
\end{array} \right.
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
m > \frac{2}{3}\\
\left[ \begin{array}{l}
m \ge 1\\
m \le – 2
\end{array} \right.
\end{array} \right. \Leftrightarrow m \ge 1.$
Chú ý: Phải có điều kiện $-m$ nằm ngoài khoảng $\left( { – 1;2} \right)$ bởi nếu $-m$ nằm trong khoảng $\left( { – 1;2} \right)$ thì hàm số bị gián đoạn trên $\left( { – 1;2} \right)$. Tức là không thể đồng biến trên $\left( { – 1;2} \right)$ được.

Ví dụ 7:  Cho hàm số $y = \frac{{mx + 2m – 3}}{{x – m}}$ ($m$ là tham số). Tìm tất cả các giá trị của $m$ sao cho hàm số nghịch biến trên khoảng $(2; + \infty )$.
Lời giải:
Tập xác định $D = R\backslash \left\{ m \right\}.$
Ta có: $y’ = \frac{{ – {m^2} – 2m + 3}}{{{{\left( {x – m} \right)}^2}}}.$
Hàm số $y = \frac{{mx + 2m – 3}}{{x – m}}$ nghịch biến trên khoảng $(2; + \infty )$ khi và chỉ khi:
$\left\{ \begin{array}{l}
y’ < 0\\
m \notin \left( {2; + \infty } \right)
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
– {m^2} – 2m + 3 < 0\\
m \le 2
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
m > 1\\
m < – 3
\end{array} \right.\\
m \le 2
\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l}
1 < m \le 2\\
m < – 3
\end{array} \right.$
Phân tích: Ở đây nhiều đọc giả không xét điều kiện để hàm số luôn xác định trên $(2; + \infty )$ là sai.