Lý thuyết đồng biến, nghịch biến của hàm số

1. Định nghĩa

Kí hiệu: K là một khoảng, một đoạn hoặc một nửa khoảng.

Cho hàm số \(y=f(x)\) xác định trên K.

• Hàm số \(y=f(x)\) đồng biến (tăng) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})\).
• Hàm số \(y=f(x)\) nghịch biến (giảm) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) > f({x_2})\).

2. Điều kiện cần để hàm số đơn điệu

Cho hàm số \(y=f(x)\) có đạo hàm trên K:

• Nếu \(f(x)\) đồng biến trên K thì \(f'(x)\geq 0\) với mọi \(x\in K\).
• Nếu \(f(x)\) nghịch biến trên K thì \(f'(x)\leq 0\) với mọi \(x\in K\).

3. Điều kiện đủ để hàm số đơn điệu

Cho hàm số \(y=f(x)\) có đạo hàm trên K:

• Nếu \(f'(x)\geq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) đồng biến trên K.
• Nếu \(f'(x)\leq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) nghịch biến trên K.
• Nếu \(f'(x)=0\) với mọi \(x\in K\) thì \(f(x)\) là hàm hằng trên K.

4. Các bước xét tính đơn điệu của hàm số

• Bước 1 : Tìm tập xác định
• Bước 2:  Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
• Bước 3:  Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.
• Bước 4:  Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Chú ý:
1) Dấu của f(x) = ax + b (\(a\neq 0\))

2) Dấu của f(x) = ax² + bx + c (\(a\neq 0\))
\(\Delta <0\) thì f(x) cùng dấu a  
\(\Delta =0\) thì f(x) cùng dấu với a 
\(\forall x\neq -\frac{b}{2a}(f(-\frac{b}{2a})=0)\)
\(\Delta >0\) thì f(x) = 0 có 2 nghiệm \(x_1.x_2(x_1<x_2)\)

Quy tắc:   “Trong trái Ngoài cùng”

Trả lời câu hỏi SGK bài 1 Giải tích 12

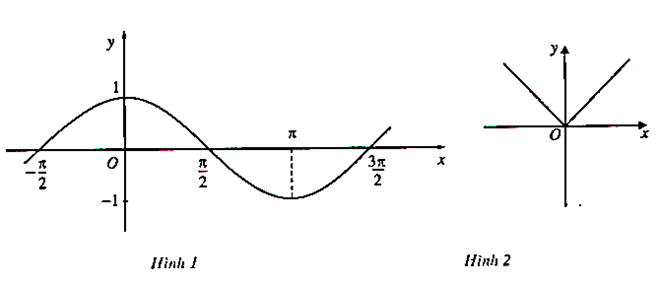
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 4: Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn $[ \frac{-\pi}{2}; \frac{3\pi}{2}]$ và các hàm số y = |x| trên khoảng (-∞; +∞).

Lời giải:

– Hàm số y = cosx trên đoạn $[ \frac{-\pi}{2}; \frac{3\pi}{2}]$:

Các khoảng tăng: [(-π)/2,0], [π, 3π/2].

Các khoảng giảm: [0, π ],.

– Hàm số y = |x| trên khoảng (-∞; +∞)

Khoảng tăng: [0, +∞)

Khoảng giảm (-∞, 0].

---

 

Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 5: Xét các hàm số sau và đồ thị của chúng:

a) $y = \frac{-x^2}{2}$ (H.4a)       b) $y = \frac{1}{x} $ (H.4b)

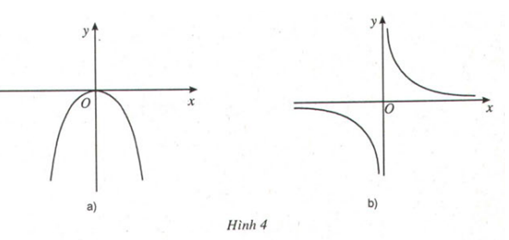
Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng.

Lời giải:

---

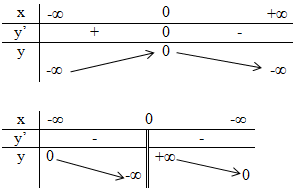
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 7: Khẳng định ngược lại với định lí trên có đúng không ? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không ?

Lời giải:

Xét hàm số y = x³ có đạo hàm y’ = 3x² ≥ 0 với mọi số thực x và hàm số đồng biến trên toàn bộ R. Vậy khẳng định ngược lại với định lý trên chưa chắc đúng hay nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó không nhất thiết phải dương (âm) trên đó.