Đồng biến, nghịch biến của hàm số khác

Đồng biến, nghịch biến của hàm số khác

Các bước xét tính đơn điệu của hàm số

• Bước 1 : Tìm tập xác định
• Bước 2:  Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
• Bước 3:  Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.
• Bước 4:  Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Ví dụ 1 . Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

\(y=\frac{x+1}{x-1}\)

• Xét hàm số \(y=\frac{x+1}{x-1}\).
  • TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
  • \(y’ = \frac{{ – 2}}{{{{(x – 1)}^2}}} > 0,\forall \ne 1\)
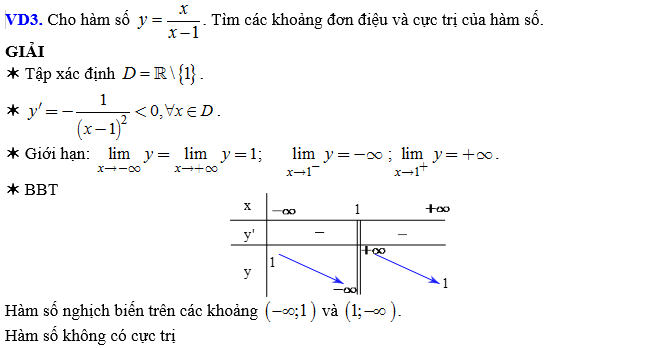
• Bảng biến thiên:

• Kết luận: Hàm số nghịch biến trên các khoảng \(\left( { – \infty ;1} \right)\) và \(\left( { 1;+ \infty } \right)\).

Ví dụ 2 . Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:

$y = \frac{{x – 2}}{{x – 1}}.$

TXĐ: $D = R\backslash \left\{ 1 \right\}.$
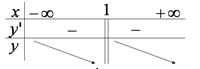
Ta có: $y’ = \frac{1}{{{{(x – 1)}^2}}} > 0,\forall x \in D$, $y’$ không xác định tại ${\rm{x}} = {\rm{1}}.$

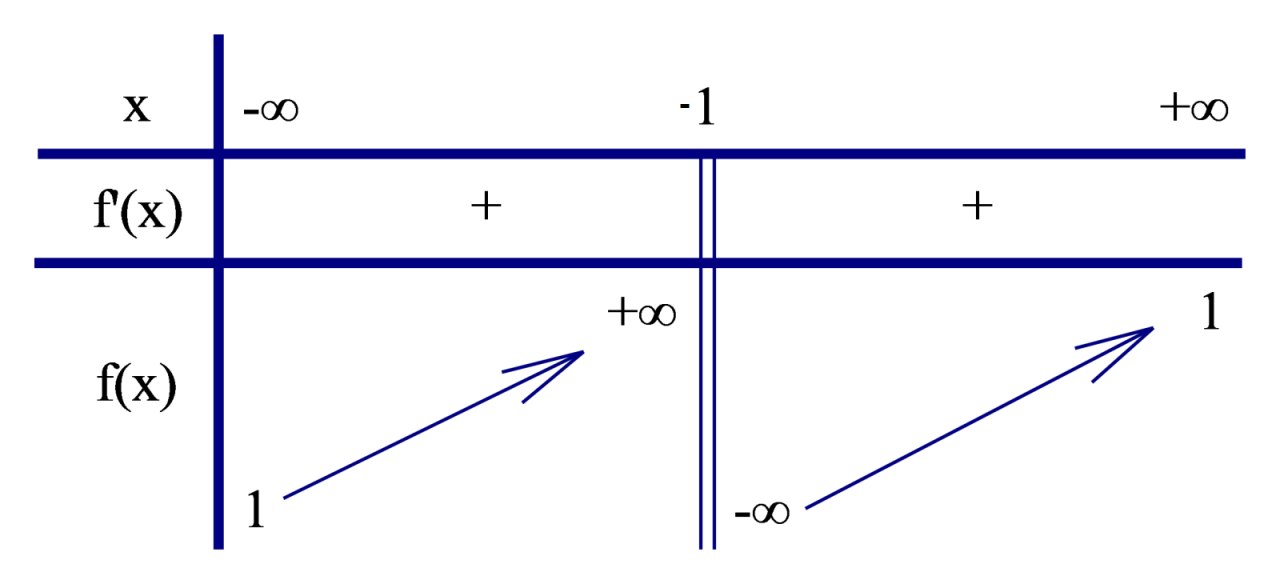
Vậy hàm số $y$ đồng biến trên mỗi khoảng $\left( { – \infty ;1} \right)$ và $\left( {1; + \infty } \right)$ (hay hàm số $y$ đồng  biến trên mỗi khoảng xác định).

—
Ví dụ 4. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:
a. $y = \frac{{{x^2} + 4x + 4}}{{x + 1}}.$
b. $y = \frac{{4{x^2} + 5x + 5}}{{x + 1}}.$

a. TXĐ: $D = R\backslash \left\{ { – 1} \right\}.$
Ta có: $y’ = \frac{{{x^2} + 2x}}{{{{(x + 1)}^2}}}$ $ \Rightarrow y’ = 0 \Leftrightarrow x = – 2,x = 0.$
Giới hạn: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $ và $\mathop {\lim }\limits_{x \to + \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to – {1^ – }} y = – \infty $ và $\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty .$
Bảng biến thiên:

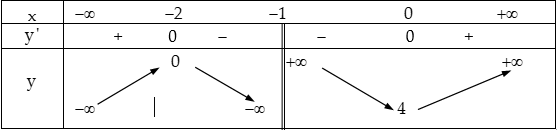
Vậy hàm số $y$ đồng biến trên mỗi khoảng: $( – \infty ; – 2)$ và $(0; + \infty )$, nghịch biến trên mỗi khoảng: $( – 2; – 1)$ và $( – 1;0)$.

b. TXĐ: $D = R\backslash \left\{ { – 1} \right\}.$
Ta có: $y’ = \frac{{4{x^2} + 8x}}{{{{(x + 1)}^2}}}$ $ \Rightarrow y’ = 0 \Leftrightarrow 4{x^2} + 8x = 0$ $ \Leftrightarrow x = 0,x = – 2.$
Giới hạn: $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $ và $\mathop {\lim }\limits_{x \to + \infty } y = + \infty $, $\mathop {\lim }\limits_{x \to – {1^ – }} y = – \infty $ và $\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty .$
Bảng biến thiên:

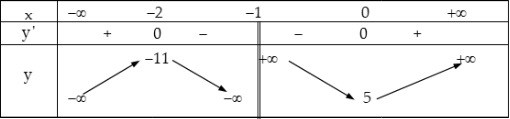
Vậy hàm số $y$ đồng biến trên mỗi khoảng: $( – \infty ; – 2)$ và $(0; + \infty )$, nghịch biến trên mỗi khoảng: $( – 2; – 1)$ và $( – 1;0).$

Ví dụ 5. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:
a. $y = \left| {{x^2} – 2x – 3} \right|.$
b. $y = \left| {{x^2} – 4x + 3} \right| + 2x + 3.$
a. TXĐ: $D = R.$
Ta có: $y = \sqrt {{{({x^2} – 2x – 3)}^2}} $ $ \Rightarrow y’ = \frac{{2(x – 1)({x^2} – 2x – 3)}}{{\sqrt {{{({x^2} – 2x – 3)}^2}} }}.$
$y’ = 0 \Leftrightarrow x = 1$, hàm số không có đạo hàm tại $x = – 1, x = 3$ (tham khảo lời giải thích ở ý b).
Bảng xét dấu:

Vậy hàm số $y$ đồng biến trên mỗi khoảng: $( – 1;1)$ và $(3; + \infty )$, nghịch biến trên: $( – \infty ; – 1)$ và $(1;3).$
Nhận xét:
+ Bài toán xét tính đơn điệu của hàm số được chuyển về bài toán xét dấu của một biểu thức $y’.$
+ Khi tính đạo hàm của hàm số có dạng $y = \left| {f(x)} \right|$ ta chuyển trị tuyệt đối vào trong căn thức $y = \sqrt {{f^2}(x)} $, khi đó tại những điểm mà $f(x) = 0$ thì hàm số không có đạo hàm.
b. TXĐ: $D = R.$
Ta có: $y = {x^2} – 4x + 3 + 4x + 3$ $ = {x^2} + 6$ khi $x \le 1 \vee x \ge 3$ và $y = – {x^2} + 4x – 3 + 4x + 3$ $ = – {x^2} + 8x$ khi $1 \le x \le 3.$
Khi $x \in ( – \infty ;1) \cup (3; + \infty )$ thì: $y’ = 2x \Rightarrow y’ = 0$ $ \Leftrightarrow x = 0 \in ( – \infty ;1) \cup (3; + \infty ).$
Khi $x \in (1;3)$ thì: $y’ = – 2x + 8$ $ \Rightarrow y’ = 0 \Leftrightarrow x = 4 \notin (1;3).$
Tại $x = 1$, ta có: $\left\{ \begin{array}{l}
f'({1^ + }) = 6\\
f'({1^ – }) = 2
\end{array} \right.$. Vì $f'({1^ + }) \ne f'({1^ – })$ nên $f’(1)$ không tồn tại.
Tại $x = 3$, ta có: $\left\{ \begin{array}{l}
f'({3^ + }) = 6\\
f'({3^ – }) = 2
\end{array} \right.$ nên $f'(3)$ không tồn tại.
Vậy hàm số $y$ đồng biến trên khoảng $(0; + \infty )$ và nghịch biến trên khoảng $( – \infty ;0).$

Ví dụ 6. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:
a. $y = \frac{{4x + 5}}{{4{x^2} – 4}}.$
b. $y = \frac{{12x + 1}}{{12{x^2} + 2}}.$
c. $y = \frac{{3{x^2} – x + 1}}{{{x^2} – x + 1}}.$

a. TXĐ: $D = R\backslash \left\{ { – 1;1} \right\}.$
Ta có: $y’ = \frac{{ – 16{x^2} – 40x – 16}}{{{{\left( {4{x^2} – 4} \right)}^2}}}$ $ \Rightarrow y’ = 0$ ⇔ $x = – 2$ hoặc $x = – \frac{1}{2}.$
Vậy, hàm số $y$ đồng biến trên các khoảng $\left( { – 2; – 1} \right)$, $\left( { – 1; – \frac{1}{2}} \right)$ và nghịch biến trên các khoảng $\left( { – \infty ; – 2} \right)$, $\left( { – \frac{1}{2};1} \right)$, $\left( {1; + \infty } \right).$
b. TXĐ: $D = R.$
Ta có: $y’ = \frac{{ – 36{x^2} – 6x + 6}}{{{{\left( {6{x^2} + 1} \right)}^2}}}.$ Với $\forall x \in R: y’ = 0$ ⇔ $x = – \frac{1}{2}$ hoặc $x = \frac{1}{3}.$
Bảng xét dấu:

Trên khoảng $\left( { – \frac{1}{2};\frac{1}{3}} \right)$: $y’ > 0$ $ \Rightarrow y$ đồng biến trên khoảng $\left( { – \frac{1}{2};\frac{1}{3}} \right).$
Trên khoảng $\left( { – \infty ; – \frac{1}{2}} \right)$ và $\left( {\frac{1}{3}; + \infty } \right)$: $y’ < 0$ $ \Rightarrow y$ nghịch biến trên các khoảng $\left( { – \infty ; – \frac{1}{2}} \right)$ và $\left( {\frac{1}{3}; + \infty } \right).$ c. TXĐ: $D = R.$ Ta có: $y’ = \frac{{ – 2{x^2} + 4x}}{{{{\left( {{x^2} – x + 1} \right)}^2}}}.$ Với $\forall x \in R: y’ = 0$ $ \Leftrightarrow x = 0$ hoặc $x = 2.$ Trên khoảng $\left( {0;2} \right)$: $y’ > 0$ $ \Rightarrow y$ đồng biến trên khoảng $\left( {0;2} \right).$
Trên khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$: $y’ < 0$ $ \Rightarrow y$ nghịch biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right).$ Ví dụ 7. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số: a. ${\rm{y}} = {\rm{x}} + \sqrt {2x – {x^2}} .$ b. $y = \left( {2x + 1} \right)\sqrt {9 – {x^2}} .$ c. $y = \sqrt {{x^2} – x – 20} .$ a. TXĐ: $D = \left[ {0;{\rm{2}}} \right].$ Ta có: $y’ = 1 + \frac{{1 – x}}{{\sqrt {2x – {x^2}} }}$ $ = \frac{{\sqrt {2x – {x^2}} + 1 – x}}{{\sqrt {2x – {x^2}} }}.$ $y’ = 0$ $ \Leftrightarrow \sqrt {2x – {x^2}} = x – 1$ $ \Leftrightarrow \left\{ \begin{array}{l} x \ge 1\\ 2x – {x^2} = {(x – 1)^2} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x \ge 1\\ 2{x^2} – 4x + 1 = 0 \end{array} \right.$ $ \Leftrightarrow x = 1 + \frac{{\sqrt 2 }}{2}.$ Vậy, hàm số $y$ đồng biến trên $\left( {0;1 + \frac{{\sqrt 2 }}{2}} \right)$ và nghịch biến trên $\left( {1 + \frac{{\sqrt 2 }}{2};2} \right).$ b. TXĐ: $D = \left[ { – 3;3} \right].$ Ta có: $y’ = 2\sqrt {9 – {x^2}} – \frac{{x\left( {2x + 1} \right)}}{{\sqrt {9 – {x^2}} }}$ $ = \frac{{ – 4{x^2} – x + 18}}{{\sqrt {9 – {x^2}} }}.$ Hàm số đã cho không có đạo hàm tại $x = – 3$ và $x = 3.$ Với $\forall x \in \left( { – 3;3} \right)$: $y’ = 0 \Leftrightarrow x = – \frac{9}{4}$ hoặc $x = 2.$ Bảng biến thiên:

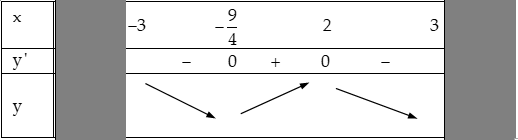
Vậy, hàm số $y$ giảm trên các khoảng $\left( { – 3; – \frac{9}{4}} \right)$, $\left( {2;3} \right)$ và tăng trên khoảng $\left( { – \frac{9}{4};2} \right).$
c. TXĐ: $D = ( – \infty ; – 4] \cup [5; + \infty ).$
Ta có: $y’ = \frac{{2x – 1}}{{2\sqrt {{x^2} – x – 20} }}$ $ \Rightarrow y’ = 0$ $ \Leftrightarrow \left\{ \begin{array}{l}
2x – 1 = 0\\
x < – 4 \vee x > 5
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{1}{2}\\
x < – 4 \vee x > 5
\end{array} \right.$

Nên phương trình $y’ = 0$ vô nghiệm.
Vậy hàm số $y$ đồng biến trên khoảng $(5; + \infty )$ và nghịch biến trên $( – \infty ; – 4).$

Ví dụ 8. Tìm các khoảng đồng biến, nghịch biến (hoặc xét chiều biến thiên) của hàm số:
a. $y = 2\sin x + \cos 2x$ với $x \in \left[ {0;\pi } \right].$
b. $y = \sin 2x – 2\cos x – 2x$ với $x \in \left( { – \frac{\pi }{2};\frac{\pi }{2}} \right).$

a. Hàm số đã cho xác định trên đoạn $\left[ {0;\pi } \right].$
Ta có: $y’ = 2\cos x\left( {1 – 2\sin x} \right).$ Ta cần tìm nghiệm của phương trình $y’ = 0$ trên khoảng $\left( {0;\pi } \right).$
$y’ = 0 \Leftrightarrow x \in \left( {0;\pi } \right)$: $\left[ \begin{array}{l}
\cos x = 0\\
\sin x = \frac{1}{2}
\end{array} \right.$ $ \Leftrightarrow x = \frac{\pi }{2}, x = \frac{\pi }{6}, x = \frac{{5\pi }}{6}.$
Bảng biến thiên:

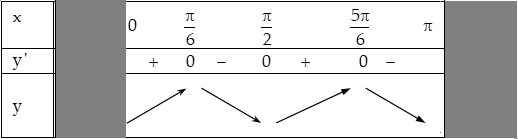
Dựa vào bảng biến thiên suy ra: hàm số đồng biến trên các khoảng $\left( {0;\frac{\pi }{6}} \right)$ và $\left( {\frac{\pi }{2};\frac{{5\pi }}{6}} \right)$, nghịch biến trên các khoảng $\left( {\frac{\pi }{6};\frac{\pi }{2}} \right)$ và $\left( {\frac{{5\pi }}{6};\pi } \right).$
b. Hàm số đã cho xác định trên khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right).$
Ta có: $y’ = 2\cos 2x + 2\sin x – 2$ $ = 2\left( {1 – 2{{\sin }^2}x} \right) + 2\sin x – 2.$
$y’ = – 2\sin x\left( {2\sin x – 1} \right).$
Trên khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)$: $y’ = 0$ $ \Leftrightarrow \left\{ \begin{array}{l}
x \in \left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\\
– 2\sin x\left( {2\sin x – 1} \right) = 0
\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \frac{\pi }{6}
\end{array} \right.$
Bảng biến thiên:

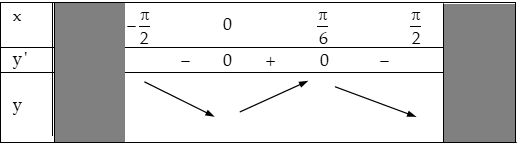
Hàm số giảm trên các khoảng $\left( { – \frac{\pi }{2};0} \right)$, $\left( {\frac{\pi }{6};\frac{\pi }{2}} \right)$ và tăng trên khoảng $\left( {0;\frac{\pi }{6}} \right).$