Trên một mảnh giấy vẽ hình tròn có bán kính bằng 2, vẽ chồng lên trên đó một hình vuông có 1 đỉnh là tâm của hình tròn và 2 đỉnh khác nằm trên đường tròn (hình vẽ bên dưới). Tính thể tích khối tròn xoay tạo ra khi quay hình đó quanh trục đối xứng của nó. A. \(\frac{{\left( {16 + 24\sqrt 2 } \right)\pi }}{3}\). B. \(\frac{{\left( {16 + 12\sqrt 2 } \right)\pi … [Đọc thêm...] vềTrên một mảnh giấy vẽ hình tròn có bán kính bằng 2, vẽ chồng lên trên đó một hình vuông có 1 đỉnh là tâm của hình tròn và 2 đỉnh khác nằm trên đường tròn (hình vẽ bên dưới). Tính thể tích khối tròn xoay tạo ra khi quay hình đó quanh trục đối xứng của nó.
Ung dung tich phan 2024
Trên một mảnh giấy vẽ hình tròn có bán kính bằng 2, vẽ chồng lên trên đó một hình vuông có 1 đỉnh là tâm của hình tròn và 2 đỉnh khác nằm trên đường tròn (hình vẽ bên dưới). Tính thể tích khối tròn xoay tạo ra khi quay hình đó quanh trục đối xứng của nó.
Từ một khúc gỗ hình trụ có đường kính \(40cm\) người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc \({60^0}\) để lấy một hình nêm (Xem hình minh họa dưới đây). Ký hiệu \(V\)là thể tích của nêm ( Hình 2). Tính \(V\)
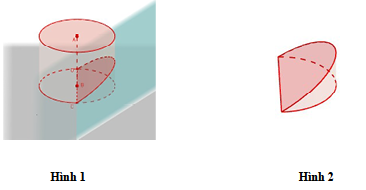
Từ một khúc gỗ hình trụ có đường kính \(40cm\) người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc \({60^0}\) để lấy một hình nêm (Xem hình minh họa dưới đây). Ký hiệu \(V\)là thể tích của nêm ( Hình 2). Tính \(V\) A. \(V = \frac{{400\sqrt 3 \pi }}{4}\left( {c{m^3}} \right)\). B. \(V = 2250\left( {c{m^3}} \right)\). C. \(V … [Đọc thêm...] vềTừ một khúc gỗ hình trụ có đường kính \(40cm\) người ta cắt khúc gỗ bởi một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc \({60^0}\) để lấy một hình nêm (Xem hình minh họa dưới đây). Ký hiệu \(V\)là thể tích của nêm ( Hình 2). Tính \(V\)
Một người có miếng đất hình tròn có bán kính bằng \(5\) m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên cần có 1 khoảng trống để dựng 1 cái chòi và để đồ dùng nên người này bớt lại 1 phần đất nhỏ không trồng cây (phần màu trắng như hình vẽ), trong đó \(AB = 6m\). Hỏi khi thu hoạch cây thì người này thu được bao nhiêu tiền ?
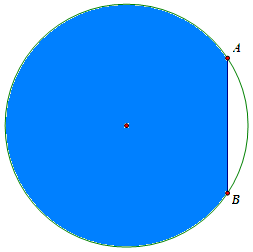
Một người có miếng đất hình tròn có bán kính bằng \(5\) m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên cần có 1 khoảng trống để dựng 1 cái chòi và để đồ dùng nên người này bớt lại 1 phần đất nhỏ không trồng cây (phần màu trắng như hình vẽ), trong đó \(AB = 6m\). Hỏi khi thu hoạch cây thì người này thu được bao … [Đọc thêm...] vềMột người có miếng đất hình tròn có bán kính bằng \(5\) m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên cần có 1 khoảng trống để dựng 1 cái chòi và để đồ dùng nên người này bớt lại 1 phần đất nhỏ không trồng cây (phần màu trắng như hình vẽ), trong đó \(AB = 6m\). Hỏi khi thu hoạch cây thì người này thu được bao nhiêu tiền ?
Để tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, – 7} \right)\), điểm \(A\left( { – 7\,;\, – 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( {15\,;\, – 2,5} \right)\) thuộc đồ thị \(y = f\left( x \right)\). Tính thể tích xấp xỉ của lọ gốm (làm tròn đến hàng đơn vị).

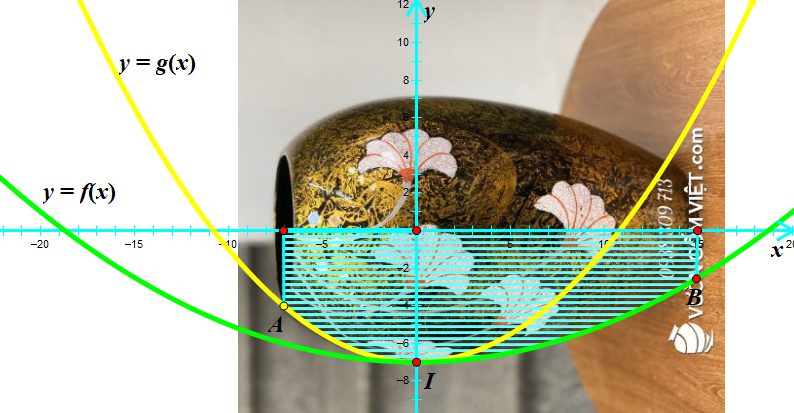
Để tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, - 7} \right)\), điểm \(A\left( { - 7\,;\, - 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( … [Đọc thêm...] vềĐể tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, – 7} \right)\), điểm \(A\left( { – 7\,;\, – 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( {15\,;\, – 2,5} \right)\) thuộc đồ thị \(y = f\left( x \right)\). Tính thể tích xấp xỉ của lọ gốm (làm tròn đến hàng đơn vị).
ột biển cảnh báo có dạng hình elip với bốn đỉnh \({A_1},{A_2},{B_1},{B_2}\)như hình vẽ dưới phần tô màu chi phí là 150.000 đồng trên một mét vuông, phần còn lại chi phí là 100.000 đồng trên một mét vuông. Hỏi số tiền ( tính theo đồng) phần tô màu gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 10m,{B_1}{B_2} = 8m\), và tứ giác \(MNPQ\)là hình chữ nhật có \(MQ = 4m\)?
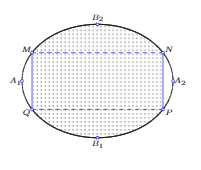
ột biển cảnh báo có dạng hình elip với bốn đỉnh \({A_1},{A_2},{B_1},{B_2}\)như hình vẽ dưới phần tô màu chi phí là 150.000 đồng trên một mét vuông, phần còn lại chi phí là 100.000 đồng trên một mét vuông. Hỏi số tiền ( tính theo đồng) phần tô màu gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 10m,{B_1}{B_2} = 8m\), và tứ giác \(MNPQ\)là hình chữ nhật có \(MQ = 4m\)? … [Đọc thêm...] vềột biển cảnh báo có dạng hình elip với bốn đỉnh \({A_1},{A_2},{B_1},{B_2}\)như hình vẽ dưới phần tô màu chi phí là 150.000 đồng trên một mét vuông, phần còn lại chi phí là 100.000 đồng trên một mét vuông. Hỏi số tiền ( tính theo đồng) phần tô màu gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 10m,{B_1}{B_2} = 8m\), và tứ giác \(MNPQ\)là hình chữ nhật có \(MQ = 4m\)?
Trong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi \({S_1},\,{S_2}\) lần lượt là diện tích của 2 miền chấm bi, gạch chéo như hình vẽ.
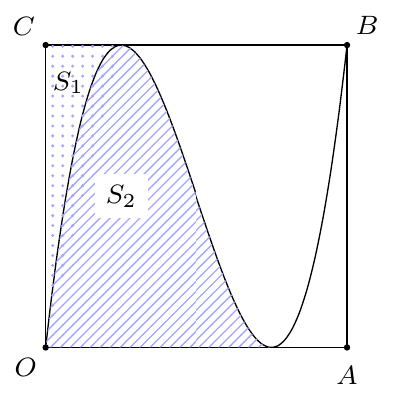
Đặt \(k = \frac{{{S_2}}}{{{S_1}}}\) và \(T = 2025k – 2024\). Khẳng định nào sau đây là đúng?
Trong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi … [Đọc thêm...] vềTrong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi \({S_1},\,{S_2}\) lần lượt là diện tích của 2 miền chấm bi, gạch chéo như hình vẽ.
Đặt \(k = \frac{{{S_2}}}{{{S_1}}}\) và \(T = 2025k – 2024\). Khẳng định nào sau đây là đúng?
Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền \((R)\) (phần được tô màu trong hình vẽ bên) quanh trục \(AB\). Miền \((R)\) được giới hạn bởi các cạnh \(AB\), \(AD\) của hình vuông \(ABCD\) và các cung phần tư của các đường tròn bán kính bằng \(1\) cm với tâm lần lượt là trung điểm của các cạnh \(AD\), \(AB\).

Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười.
Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền \((R)\) (phần được tô màu trong hình vẽ bên) quanh trục \(AB\). Miền \((R)\) được giới hạn bởi các cạnh \(AB\), \(AD\) của hình vuông \(ABCD\) và các cung phần tư của các đường tròn bán kính bằng \(1\) cm với tâm lần lượt là trung điểm của các cạnh \(AD\), \(AB\). Tính thể tích của vật trang trí … [Đọc thêm...] vềMột vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền \((R)\) (phần được tô màu trong hình vẽ bên) quanh trục \(AB\). Miền \((R)\) được giới hạn bởi các cạnh \(AB\), \(AD\) của hình vuông \(ABCD\) và các cung phần tư của các đường tròn bán kính bằng \(1\) cm với tâm lần lượt là trung điểm của các cạnh \(AD\), \(AB\).
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười.
Cho hai đường tròn \(\left( {{O_1};5} \right)\) và \(\left( {{O_2};3} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};3} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục \({O_1}{O_2}\) ta được một khối tròn xoay. Tính thể tích \(V\) của khối tròn xoay được tạo thành.

Cho hai đường tròn \(\left( {{O_1};5} \right)\) và \(\left( {{O_2};3} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};3} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục \({O_1}{O_2}\) ta … [Đọc thêm...] vềCho hai đường tròn \(\left( {{O_1};5} \right)\) và \(\left( {{O_2};3} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};3} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục \({O_1}{O_2}\) ta được một khối tròn xoay. Tính thể tích \(V\) của khối tròn xoay được tạo thành.
Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm.

Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm. A. \(1250{\pi … [Đọc thêm...] vềSăm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm.
Một mảnh đất hình chữ nhật có chiều dài \(60\,m\), chiều rộng \(20\,m\). Người ta muốn trồng cỏ ở hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường parabol có hai đỉnh cách nhau \(40\,m\) (như hình vẽ bên dưới). Phần còn lại của mảnh đất người ta lát gạch. Biết chi phí lát gạch là \(200.000\)đồng/\({m^2}\) và tiền nhân công trồng cỏ là \(100.000\) đồng/\({m^2}\). Tính tổng số tiền để lát gạch và trồng cỏ trên mảnh đất đó (làm tròn đến hàng nghìn).

Một mảnh đất hình chữ nhật có chiều dài \(60\,m\), chiều rộng \(20\,m\). Người ta muốn trồng cỏ ở hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường parabol có hai đỉnh cách nhau \(40\,m\) (như hình vẽ bên dưới). Phần còn lại của mảnh đất người ta lát gạch. Biết chi phí lát gạch là \(200.000\)đồng/\({m^2}\) và tiền nhân công trồng cỏ là \(100.000\) đồng/\({m^2}\). … [Đọc thêm...] vềMột mảnh đất hình chữ nhật có chiều dài \(60\,m\), chiều rộng \(20\,m\). Người ta muốn trồng cỏ ở hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường parabol có hai đỉnh cách nhau \(40\,m\) (như hình vẽ bên dưới). Phần còn lại của mảnh đất người ta lát gạch. Biết chi phí lát gạch là \(200.000\)đồng/\({m^2}\) và tiền nhân công trồng cỏ là \(100.000\) đồng/\({m^2}\). Tính tổng số tiền để lát gạch và trồng cỏ trên mảnh đất đó (làm tròn đến hàng nghìn).
