Từ một tấm tôn hình chữ nhật \(ABCD\) với \(AB = 30\,cm,AD = \frac{{55\pi }}{3}\,cm\). Người ta cắt miếng tôn theo đường hình \(\sin \) như hình vẽ bên để được hai miếng tôn nhỏ. Biết \(AM = 20\,cm\),\(CN = 15\,cm\),\(BE = 5\pi \,cm\).Tính thể tích của lọ hoa được tạo thành bằng cách quay miếng tôn lớn quanh trục \(AD\) (kết quả làm tròn đến hàng trăm). A. … [Đọc thêm...] vềTừ một tấm tôn hình chữ nhật \(ABCD\) với \(AB = 30\,cm,AD = \frac{{55\pi }}{3}\,cm\). Người ta cắt miếng tôn theo đường hình \(\sin \) như hình vẽ bên để được hai miếng tôn nhỏ. Biết \(AM = 20\,cm\),\(CN = 15\,cm\),\(BE = 5\pi \,cm\).Tính thể tích của lọ hoa được tạo thành bằng cách quay miếng tôn lớn quanh trục \(AD\) (kết quả làm tròn đến hàng trăm).
Ung dung tich phan 2024
Từ một tấm tôn hình chữ nhật \(ABCD\) với \(AB = 30\,cm,AD = \frac{{55\pi }}{3}\,cm\). Người ta cắt miếng tôn theo đường hình \(\sin \) như hình vẽ bên để được hai miếng tôn nhỏ. Biết \(AM = 20\,cm\),\(CN = 15\,cm\),\(BE = 5\pi \,cm\).Tính thể tích của lọ hoa được tạo thành bằng cách quay miếng tôn lớn quanh trục \(AD\) (kết quả làm tròn đến hàng trăm).
Gọi \(\left( D \right)\) là diện tích hình phẳng được giới hạn bởi hai đường cong \(y = f\left( x \right) = a{x^2} + bx + c\) và \(y = g\left( x \right) = – {x^2} + mx + n\) (như hình vẽ).

Biết \({S_{\left( D \right)}} = 9\) và đồ thị hàm số \(y = g\left( x \right)\) có đỉnh \(I\left( {0;2} \right)\). Khi cho miền được giới hạn bởi hai đường cong trên và hai đường thẳng \(x = – 1;\,x = 2\) quay quanh trục \(Ox\), ta nhận được vật thể tròn xoay có thể tích \(V\). Giá trị của \(V\) bằng
Gọi \(\left( D \right)\) là diện tích hình phẳng được giới hạn bởi hai đường cong \(y = f\left( x \right) = a{x^2} + bx + c\) và \(y = g\left( x \right) = - {x^2} + mx + n\) (như hình vẽ). Biết \({S_{\left( D \right)}} = 9\) và đồ thị hàm số \(y = g\left( x \right)\) có đỉnh \(I\left( {0;2} \right)\). Khi cho miền được giới hạn bởi hai đường cong trên và hai đường thẳng … [Đọc thêm...] vềGọi \(\left( D \right)\) là diện tích hình phẳng được giới hạn bởi hai đường cong \(y = f\left( x \right) = a{x^2} + bx + c\) và \(y = g\left( x \right) = – {x^2} + mx + n\) (như hình vẽ).
Biết \({S_{\left( D \right)}} = 9\) và đồ thị hàm số \(y = g\left( x \right)\) có đỉnh \(I\left( {0;2} \right)\). Khi cho miền được giới hạn bởi hai đường cong trên và hai đường thẳng \(x = – 1;\,x = 2\) quay quanh trục \(Ox\), ta nhận được vật thể tròn xoay có thể tích \(V\). Giá trị của \(V\) bằng
Một cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng \({\rm{1m}}\), trục bé bằng \({\rm{0}}{\rm{,8m}}\), chiều dài (mặt trong của thùng) bằng \({\rm{3m}}\). Thùng đươc đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là \({\rm{0}}{\rm{,6m}}\). Tính thể tích \(V\)của dầu có trong thùng (Kết quả làm tròn đến phần trăm).

Một cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng \({\rm{1m}}\), trục bé bằng \({\rm{0}}{\rm{,8m}}\), chiều dài (mặt trong của thùng) bằng \({\rm{3m}}\). Thùng đươc đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là \({\rm{0}}{\rm{,6m}}\). … [Đọc thêm...] vềMột cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng \({\rm{1m}}\), trục bé bằng \({\rm{0}}{\rm{,8m}}\), chiều dài (mặt trong của thùng) bằng \({\rm{3m}}\). Thùng đươc đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là \({\rm{0}}{\rm{,6m}}\). Tính thể tích \(V\)của dầu có trong thùng (Kết quả làm tròn đến phần trăm).
Hình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó.

Hình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó. A. \(\frac{{4\pi \sqrt 3 }}{3}\). B. \(\frac{{4\sqrt 3 }}{3}\). C. \(\frac{{2\sqrt 3 }}{3}\). D. \(\frac{{2\pi \sqrt 3 }}{3}\). Lời giải: Trên mặt phẳng đáy của vật rắn, chọn hệ trục … [Đọc thêm...] vềHình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó.
Trong đợt tổ chức HKPĐ cấp tỉnh lần thứ XIV, ban tổ chức thiết kế một cổng chào bằng phao chứa không khí ở bên trong, có hình dạng như một nửa cái Săm ô tô khi bơm căng (tham khảo hình vẽ). Cổng chào có chiều cao so với mặt sân là \(9m\) (tính cả phần phao chứa không khí), phần chân của cổng chào tiếp xúc với mặt sân theo một đường tròn có đường kính là \(2m\) và bề rộng của cổng chào là \(18m\) (tính cả phần phao chứa không khí). Bỏ qua độ dày của lớp vỏ cổng chào, mặt sân coi là bằng phẳng. Tính thể tích không khí chứa bên trong cổng chào.


Trong đợt tổ chức HKPĐ cấp tỉnh lần thứ XIV, ban tổ chức thiết kế một cổng chào bằng phao chứa không khí ở bên trong, có hình dạng như một nửa cái Săm ô tô khi bơm căng (tham khảo hình vẽ). Cổng chào có chiều cao so với mặt sân là \(9m\) (tính cả phần phao chứa không khí), phần chân của cổng chào tiếp xúc với mặt sân theo một đường tròn có đường kính là \(2m\) và bề rộng của … [Đọc thêm...] vềTrong đợt tổ chức HKPĐ cấp tỉnh lần thứ XIV, ban tổ chức thiết kế một cổng chào bằng phao chứa không khí ở bên trong, có hình dạng như một nửa cái Săm ô tô khi bơm căng (tham khảo hình vẽ). Cổng chào có chiều cao so với mặt sân là \(9m\) (tính cả phần phao chứa không khí), phần chân của cổng chào tiếp xúc với mặt sân theo một đường tròn có đường kính là \(2m\) và bề rộng của cổng chào là \(18m\) (tính cả phần phao chứa không khí). Bỏ qua độ dày của lớp vỏ cổng chào, mặt sân coi là bằng phẳng. Tính thể tích không khí chứa bên trong cổng chào.
Cho hình vuông có độ dài cạnh bằng \(8{\rm{cm}}\) và một hình tròn có bán kính \(5{\rm{cm}}\) được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Tính thể tích \(V\) của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục \(XY.\)

Cho hình vuông có độ dài cạnh bằng \(8{\rm{cm}}\) và một hình tròn có bán kính \(5{\rm{cm}}\) được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Tính thể tích \(V\) của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục \(XY.\) A. \(V = \frac{{260\pi }}{3}{\rm{c}}{{\rm{m}}^{\rm{3}}}\). B. \(V = \frac{{290\pi … [Đọc thêm...] vềCho hình vuông có độ dài cạnh bằng \(8{\rm{cm}}\) và một hình tròn có bán kính \(5{\rm{cm}}\) được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Tính thể tích \(V\) của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục \(XY.\)
Trong mặt phẳng cho hình vuông \(ABCD\) cạnh \(2\sqrt 2 \), phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính (tham khảo hình vẽ).

Thể tích của khối tròn xoay sinh ra khi quay hình trên quanh đường thẳng \(AC\) gần nhất với kết quả nào sau đây?
Trong mặt phẳng cho hình vuông \(ABCD\) cạnh \(2\sqrt 2 \), phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính (tham khảo hình vẽ). Thể tích của khối tròn xoay sinh ra khi quay hình trên quanh đường thẳng \(AC\) gần nhất với kết quả nào sau đây? A. \(72,9\). B. \(36,5\). C. \(73,4\). D. \(145,9\). Lời … [Đọc thêm...] vềTrong mặt phẳng cho hình vuông \(ABCD\) cạnh \(2\sqrt 2 \), phía ngoài hình vuông vẽ thêm bốn nửa đường tròn nhận các cạnh của hình vuông làm đường kính (tham khảo hình vẽ).
Thể tích của khối tròn xoay sinh ra khi quay hình trên quanh đường thẳng \(AC\) gần nhất với kết quả nào sau đây?
Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.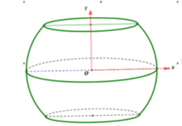
Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
A. \(\frac{{100}}{3}\pi \left( {d{m^3}} \right)\).
B. \(\frac{{43}}{3}\pi \left( … [Đọc thêm...] về Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\) A. \(\frac{5}{4}\). B. \(\frac{3}{2}\). C. \(\frac{1}{2}\). D. \(2\). Lời giải Đặt: \(y = f\left( x \right) \Rightarrow x = {y^3} + y.\) \( \Rightarrow dx = … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) – f’\left( x \right) = 3x\left( {2x – 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = – 1\). Giá trị của \(f\left( 2 \right)\) bằng
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) - f'\left( x \right) = 3x\left( {2x - 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = - 1\). Giá trị của \(f\left( 2 \right)\) bằng A. \(7\). B. \(6\). C. \(1\). D. \(2\). Lời giải Ta có: \(2f\left( x \right) - f'\left( x … [Đọc thêm...] về Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) – f’\left( x \right) = 3x\left( {2x – 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = – 1\). Giá trị của \(f\left( 2 \right)\) bằng
