Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\), \(f\left( x \right) > - 1\), \(f\left( 0 \right) = 0\), và thỏa\(f'\left( x \right)\sqrt {{x^2} + 1} = 2x\sqrt {f\left( x \right) + 1} \). Tính \(f\left( {\sqrt 3 } \right)\). A. 0 B. 3 C. 7. D. 9 Lời giải Ta có \(f'\left( x \right)\sqrt {{x^2} + 1} = 2x\sqrt … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\), \(f\left( x \right) > – 1\), \(f\left( 0 \right) = 0\), và thỏa\(f’\left( x \right)\sqrt {{x^2} + 1} = 2x\sqrt {f\left( x \right) + 1} \). Tính \(f\left( {\sqrt 3 } \right)\).
Ung dung tich phan 2024
Cho hình phẳng \(H\) giới hạn bởi các đường \(y = f\left( x \right) = {x^2} – 8x + 12\) và \(y = g\left( x \right) = – x + 6\) (phần tô đậm trong hình). Khối tròn xoay tạo thành khi quay \(H\) xung quanh trục hoành có thể tích bằng bao nhiêu?

Cho hình phẳng \(H\) giới hạn bởi các đường \(y = f\left( x \right) = {x^2} - 8x + 12\) và \(y = g\left( x \right) = - x + 6\) (phần tô đậm trong hình). Khối tròn xoay tạo thành khi quay \(H\) xung quanh trục hoành có thể tích bằng bao nhiêu?
A. \(\frac{{216\pi }}{5}\).
B. \(\frac{{949\pi }}{{15}}\).
C. \(\frac{{817\pi }}{{15}}\).
D. \(\frac{{836\pi … [Đọc thêm...] về Cho hình phẳng \(H\) giới hạn bởi các đường \(y = f\left( x \right) = {x^2} – 8x + 12\) và \(y = g\left( x \right) = – x + 6\) (phần tô đậm trong hình). Khối tròn xoay tạo thành khi quay \(H\) xung quanh trục hoành có thể tích bằng bao nhiêu?
Cho hàm số \(y = f(x)\)có đạo hàm liên tục trên đoạn \({\rm{[1}};3]\) thỏa mãn \(f(1) = 4\) và \(f(x) – (x + 3)f'(x) = 2x{f^2}(x),\forall x \in [1;3]\). Giá trị của \(\int_1^3 {f(x)dx} \)bằng
Cho hàm số \(y = f(x)\)có đạo hàm liên tục trên đoạn \({\rm{[1}};3]\) thỏa mãn \(f(1) = 4\) và \(f(x) - (x + 3)f'(x) = 2x{f^2}(x),\forall x \in [1;3]\). Giá trị của \(\int_1^3 {f(x)dx} \)bằng A. \(1 + \ln 3\). B. \(2 - \ln 3\). C. \(2 + \ln 3\). D. \(1 - \ln 3\). Lời giải + Xét \(f(x) \ne 0\), theo giả thiết ta có \(f(x) - (x + 3)f'(x) = 2x{f^2}(x)\) ⇔ … [Đọc thêm...] vềCho hàm số \(y = f(x)\)có đạo hàm liên tục trên đoạn \({\rm{[1}};3]\) thỏa mãn \(f(1) = 4\) và \(f(x) – (x + 3)f'(x) = 2x{f^2}(x),\forall x \in [1;3]\). Giá trị của \(\int_1^3 {f(x)dx} \)bằng
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { – 1;1} \right]\) và thỏa mãn \(f\left( x \right) + 2 = \frac{3}{2}\int\limits_{ – 1}^1 {\left( {x + t} \right)f\left( t \right){\rm{d}}t} \) với \(\;\forall x \in \left[ { – 1;1} \right]\). Khi đó \(I = \int\limits_{ – 1}^1 {f\left( x \right){\rm{d}}x} \) bằng
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;1} \right]\) và thỏa mãn \(f\left( x \right) + 2 = \frac{3}{2}\int\limits_{ - 1}^1 {\left( {x + t} \right)f\left( t \right){\rm{d}}t} \) với \(\;\forall x \in \left[ { - 1;1} \right]\). Khi đó \(I = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} \) bằng A. \(I = 3\). B. \(I = 4\). C. \(I = 2\). D. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { – 1;1} \right]\) và thỏa mãn \(f\left( x \right) + 2 = \frac{3}{2}\int\limits_{ – 1}^1 {\left( {x + t} \right)f\left( t \right){\rm{d}}t} \) với \(\;\forall x \in \left[ { – 1;1} \right]\). Khi đó \(I = \int\limits_{ – 1}^1 {f\left( x \right){\rm{d}}x} \) bằng
Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài \(50\,{\rm{m}}\). Để giảm bớt kinh phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ. Phần tô màu gồm hai miền diện tích bằng nhau và đường cong \(AIB\) là một parabol có đỉnh \(I.\) Phần tô màu được trồng cỏ nhân tạo với giá \(130\) nghìn đồng/\({{\rm{m}}^2}\) và phần còn lại được trồng cỏ nhân tạo với giá \(90\) nghìn đồng/\({{\rm{m}}^2}\). Hỏi ông An phải trả bao nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?
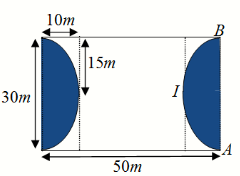

Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài \(50\,{\rm{m}}\). Để giảm bớt kinh phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ. Phần tô màu gồm hai miền diện tích bằng nhau và đường cong \(AIB\) là một parabol có đỉnh \(I.\) Phần tô màu được trồng cỏ nhân tạo với giá \(130\) nghìn … [Đọc thêm...] vềÔng An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài \(50\,{\rm{m}}\). Để giảm bớt kinh phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ. Phần tô màu gồm hai miền diện tích bằng nhau và đường cong \(AIB\) là một parabol có đỉnh \(I.\) Phần tô màu được trồng cỏ nhân tạo với giá \(130\) nghìn đồng/\({{\rm{m}}^2}\) và phần còn lại được trồng cỏ nhân tạo với giá \(90\) nghìn đồng/\({{\rm{m}}^2}\). Hỏi ông An phải trả bao nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?

Cho hai đường tròn \(\left( {{O_1};10} \right)\) và \(\left( {{O_2};6} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};6} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục \({O_1}{O_2}\) ta được một khối tròn xoay. Tính thể tích \(V\) của khối tròn xoay được tạo thành.

Cho hai đường tròn \(\left( {{O_1};10} \right)\) và \(\left( {{O_2};6} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};6} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục … [Đọc thêm...] về Cho hai đường tròn \(\left( {{O_1};10} \right)\) và \(\left( {{O_2};6} \right)\) cắt nhau tại hai điểm \(A\), \(B\)sao cho \(AB\) là một đường kính của đường tròn \(\left( {{O_2};6} \right)\). Gọi \(\left( D \right)\) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay \(\left( D \right)\) quanh trục \({O_1}{O_2}\) ta được một khối tròn xoay. Tính thể tích \(V\) của khối tròn xoay được tạo thành.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {1\,;\,2} \right]\) và thoả mãn đồng thời các điều kiện \(f\left( 1 \right) = – \frac{1}{2}\) và \(f\left( x \right) + xf’\left( x \right) = \left( {2{x^3} + {x^2}} \right){f^2}\left( x \right)\), \(\forall x \in \left[ {1\,;\,2} \right]\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục \(Ox\), \(x = 1,\) \(\,x = 2\). Khẳng định nào sau đây đúng?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {1\,;\,2} \right]\) và thoả mãn đồng thời các điều kiện \(f\left( 1 \right) = - \frac{1}{2}\) và \(f\left( x \right) + xf'\left( x \right) = \left( {2{x^3} + {x^2}} \right){f^2}\left( x \right)\), \(\forall x \in \left[ {1\,;\,2} \right]\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {1\,;\,2} \right]\) và thoả mãn đồng thời các điều kiện \(f\left( 1 \right) = – \frac{1}{2}\) và \(f\left( x \right) + xf’\left( x \right) = \left( {2{x^3} + {x^2}} \right){f^2}\left( x \right)\), \(\forall x \in \left[ {1\,;\,2} \right]\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục \(Ox\), \(x = 1,\) \(\,x = 2\). Khẳng định nào sau đây đúng?
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \({\left( {f’\left( x \right)} \right)^2} = f\left( x \right).{e^x},\forall x \in \mathbb{R}\) và \(f\left( 0 \right) = 2.\) Khi đó \(f\left( 4 \right)\) thuộc khoảng nào sau đây?
Cho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \({\left( {f'\left( x \right)} \right)^2} = f\left( x \right).{e^x},\forall x \in \mathbb{R}\) và \(f\left( 0 \right) = 2.\) Khi đó \(f\left( 4 \right)\) thuộc khoảng nào sau đây? A. \(\left( {60;62} \right)\). B. \(\left( {55;58} \right)\). C. \(\left( {7;8} … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) đồng biến và có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \({\left( {f’\left( x \right)} \right)^2} = f\left( x \right).{e^x},\forall x \in \mathbb{R}\) và \(f\left( 0 \right) = 2.\) Khi đó \(f\left( 4 \right)\) thuộc khoảng nào sau đây?
