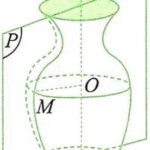
Bài toán: Một chiếc đồng hồ cát như hình vẽ gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt phằng nằm ngang. Ban đầu lượng cát dồn hết […]
_TLN ung dung tich phan
Cho đường tròn tâm $O$, bán kính bằng 2 . Trên đường tròn, lấy 6 điểm chia đều đường tròn, lần lượt là $A,B,C,D,E,F$.
Bài toán Cho đường tròn tâm $O$, bán kính bằng 2 . Trên đường tròn, lấy 6 điểm chia đều đường tròn, lần lượt là $A,B,C,D,E,F$. Vẽ cung tròn $C_{1}$ tiếp xúc với hai đoạn thẳng $OA$ và $OB$, đi qua hai điểm $A$ và $B$. Tương tự, vẽ cung tròn $C_{2}$ tiếp xúc với […]
Một quả trứng khủng long đồ chơi bằng nhựa có thiết diện qua trục lớn là một đường elip. Biết độ dài mỗi trục là 12 cm và 8 cm
Bài toán: Một quả trứng khủng long đồ chơi bằng nhựa có thiết diện qua trục lớn là một đường elip. Biết độ dài mỗi trục là 12 cm và 8 cm . Bên trong quả trứng người ta cần thiết kế một chiếc hộp hình trụ để đựng các đồ chơi trẻ con như […]
Một quả bóng bầu dục theo quy định được sử dụng trong giải bầu dục quốc gia có kích thước $28\left(\mathrm{\,\;cm}\right)$ từ đầu này đến đầu kia và đường kính $17\left(\mathrm{\,\;cm}\right)$ ở phần dày nhất
Bài toán: Một quả bóng bầu dục theo quy định được sử dụng trong giải bầu dục quốc gia có kích thước $28\left(\mathrm{\,\;cm}\right)$ từ đầu này đến đầu kia và đường kính $17\left(\mathrm{\,\;cm}\right)$ ở phần dày nhất ( quy định có phép thay đổi một chút về các kích thước này) (Nguồn: NFL). Hình dạng […]
Một bức tường hình chữ nhật $ABCD$ có kích thước $6\left(m\right),4\left(m\right)$ được bạn Hà trang trí bằng cách vẽ hai đồ thị $f\left(x\right)=a^{x},g\left(x\right)=\mathrm{\,lo}\mathrm{\,g}_{b}x$ đối xứng nhau qua đường thẳng $d:y=x$ và chia thành ba phần
Bài toán: Một bức tường hình chữ nhật $ABCD$ có kích thước $6\left(m\right),4\left(m\right)$ được bạn Hà trang trí bằng cách vẽ hai đồ thị $f\left(x\right)=a^{x},g\left(x\right)=\mathrm{\,lo}\mathrm{\,g}_{b}x$ đối xứng nhau qua đường thẳng $d:y=x$ và chia thành ba phần (tham khảo hình vẽ bên). Phần $H_{1}$ được sơn màu xanh da trời, phần $H_{2}$ được sơn màu […]
Hệ thống lọc nước bể bơi vô cùng quan trọng khi tiến hành xây dựng công trình bơi lội để nguồn nước được làm sạch thường xuyên và giữ vệ sinh cho người bơi. Trong quá trình vận hành lọc nước thì lượng nước trong bể sẽ thay đổi theo thời gian. Lượng nước trong bể giảm nếu hệ thống đang xả nước bẩn ra khỏi bể và tăng nếu hệ thống đang cấp thêm nước sạch cho bể
Bài toán: Hệ thống lọc nước bể bơi vô cùng quan trọng khi tiến hành xây dựng công trình bơi lội để nguồn nước được làm sạch thường xuyên và giữ vệ sinh cho người bơi. Trong quá trình vận hành lọc nước thì lượng nước trong bể sẽ thay đổi theo thời gian. Lượng […]
Xét phần đựng nước bên trong một lục bình có dạng mặt tròn xoay trong đó đường sinh là đường cong $\left(C\right)$ quay quanh trục $\left(d\right)$ như hình bên. Biết rằng $\left(C\right)$ là đường cong bậc ba; chiều cao phần đựng nước là 35 cm
Bài toán: Xét phần đựng nước bên trong một lục bình có dạng mặt tròn xoay trong đó đường sinh là đường cong $\left(C\right)$ quay quanh trục $\left(d\right)$ như hình bên. Biết rằng $\left(C\right)$ là đường cong bậc ba; chiều cao phần đựng nước là 35 cm ; bán kính đáy phần đựng nước là […]
Hoạ sĩ thiết kế một micro có dạng khối tròn xoay, mặt cắt đứng chứa trục của khối tròn xoay có dạng như hình sau, trong đó $OA=OB=OI=2\mathrm{\,\;cm},MC=MD=1\mathrm{\,\;cm}$, đường thẳng $OM$ là đường trung trực của đoạn thẳng $CD,OM=20\mathrm{\,\;cm},AOB=90^{\circ }$.
Bài toán: Hoạ sĩ thiết kế một micro có dạng khối tròn xoay, mặt cắt đứng chứa trục của khối tròn xoay có dạng như hình sau, trong đó $OA=OB=OI=2\mathrm{\,\;cm},MC=MD=1\mathrm{\,\;cm}$, đường thẳng $OM$ là đường trung trực của đoạn thẳng $CD,OM=20\mathrm{\,\;cm},AOB=90^{\circ }$. Thể tích của micro này là bao nhiêu $\mathrm{\,c}\mathrm{\,m}^{3}$ ? (Làm tròn kết […]
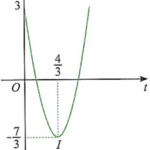
Một vật chuyển động thẳng. Khi vật bắt đầu qua điểm $O$, người ta bắt đầu quan sát, đo đạc chuyển động của vật thì thấy vận tốc tức thời của vật tại thời điểm $t\left(s\right)$ là $v\left(t\right)\left(\mathrm{\,m}/\mathrm{\,s}\right)$, hàm vận tốc $v\left(t\right)$ có đồ thị phụ thuộc thời gian là một phần của đường parabol đỉnh $I\left(\dfrac{4}{3};-\dfrac{7}{3}\right)$ như hình bên (với $t\geq 0$ và mốc tính thời gian là lúc bắt đầu quan sát chuyển động)
Bài toán: Một vật chuyển động thẳng. Khi vật bắt đầu qua điểm $O$, người ta bắt đầu quan sát, đo đạc chuyển động của vật thì thấy vận tốc tức thời của vật tại thời điểm $t\left(s\right)$ là $v\left(t\right)\left(\mathrm{\,m}/\mathrm{\,s}\right)$, hàm vận tốc $v\left(t\right)$ có đồ thị phụ thuộc thời gian là một phần của […]
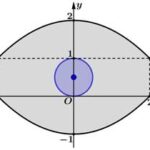
Bạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây
Bài toán: Bạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây (phần được tô màu đen) và một hình tròn có bán kính bằng $0,5\mathrm{\,dm}$ […]