Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

MAX MIN HAM GIA TRI TUYET DOI

Giá trị lớn nhất, giá trị nhỏ nhất hàm trị tuyệt đối 2023

Ngày Thuộc chủ đề:Sách toán 12 Tag với:

Giá trị lớn nhất, giá trị nhỏ nhất hàm trị tuyệt đối 2023 ========== booktoan.com chia sẻ đến các em file pdf Giá trị lớn nhất, giá trị nhỏ nhất hàm trị tuyệt đối 2023. Đề có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi HK1 năm nay. NGUỒN: BOOKTOAN.COM ———– xem file de thi … [Đọc thêm...] vềGiá trị lớn nhất, giá trị nhỏ nhất hàm trị tuyệt đối 2023

Xét hàm số \(g\left( x \right) = f\left( {2{x^3} + x – 1} \right) + m.\) Tìm \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = – 10.\)

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:,

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới. Xét hàm số \(g\left( x \right) = f\left( {2{x^3} + x - 1} \right) + m.\) Tìm \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) =  - 10.\) A. \(m =  - 13.\)              … [Đọc thêm...] vềXét hàm số \(g\left( x \right) = f\left( {2{x^3} + x – 1} \right) + m.\) Tìm \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = – 10.\)

Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) sao cho \(f(x) = \left| {{x^3} – 3x + m} \right| \le 16,\,\forall x \in \left[ {0;3} \right]\). Tổng tất cả các phần tử của \(S\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) sao cho \(f(x) = \left| {{x^3} - 3x + m} \right| \le 16,\,\forall x \in \left[ {0;3} \right]\). Tổng tất cả các phần tử của \(S\) bằng A. \( - 104\). B. \(104\). C. \( - 96\). D. \(96\). Lời giải Chọn A \(f(x) = \left| {{x^3} - 3x + m} \right| \le 16,\,\forall x \in \left[ {0;3} … [Đọc thêm...] vềGọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) sao cho \(f(x) = \left| {{x^3} – 3x + m} \right| \le 16,\,\forall x \in \left[ {0;3} \right]\). Tổng tất cả các phần tử của \(S\) bằng

Giá trị lớn nhất của hàm số \(y = \left| {\frac{{\ln x + 1}}{{\sqrt {{{\ln }^2}x + 1} }} + m} \right|\) trên \(\left[ {1;{e^2}} \right]\) đạt giá trị nhỏ nhất là bao nhiêu?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Giá trị lớn nhất của hàm số \(y = \left| {\frac{{\ln x + 1}}{{\sqrt {{{\ln }^2}x + 1} }} + m} \right|\) trên \(\left[ {1;{e^2}} \right]\) đạt giá trị nhỏ nhất là bao nhiêu? A. \(\frac{{1 + \sqrt 2 }}{2}\) B. \(\frac{{\sqrt 2 - 1}}{4}\) C. \(\frac{{1 + \sqrt 2 }}{4}\) D. \(\frac{{\sqrt 2 - 1}}{2}\) LỜI GIẢI CHI TIẾT Đặt \(t = \ln x;x \in \left[ … [Đọc thêm...] vềGiá trị lớn nhất của hàm số \(y = \left| {\frac{{\ln x + 1}}{{\sqrt {{{\ln }^2}x + 1} }} + m} \right|\) trên \(\left[ {1;{e^2}} \right]\) đạt giá trị nhỏ nhất là bao nhiêu?

Biết giá trị lớn nhất hàm số \(f\left( x \right) = \left| {{x^3} – 3{x^2} + m} \right|\) trên đoạn \(\left[ { – 1;4} \right]\) bằng 10. Khi đó mệnh đề nào sau đây đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Biết giá trị lớn nhất hàm số \(f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ { - 1;4} \right]\) bằng 10. Khi đó mệnh đề nào sau đây đúng? A. \( - 7 < m < 2.\) B. \(m > 2.\) C. \(m < - 27\,\) D. \(\frac{1}{2} < m < \frac{3}{2}.\) LỜI GIẢI CHI TIẾT + Đặt \(g\left( x \right) = {x^3} - 3{x^2} + m … [Đọc thêm...] vềBiết giá trị lớn nhất hàm số \(f\left( x \right) = \left| {{x^3} – 3{x^2} + m} \right|\) trên đoạn \(\left[ { – 1;4} \right]\) bằng 10. Khi đó mệnh đề nào sau đây đúng?

Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {{x^3} – 3{x^2} – 9x + m} \right|\) trên đoạn \(\left[ { – 2;4} \right]\) bằng \(16\). Số phần tử của \(S\) là

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {{x^3} - 3{x^2} - 9x + m} \right|\) trên đoạn \(\left[ { - 2;4} \right]\) bằng \(16\). Số phần tử của \(S\) là A. \(0\). B. \(2\). C. \(4\). D. \(1\). LỜI GIẢI CHI TIẾT Xét hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + m\) trên đoạn … [Đọc thêm...] vềGọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {{x^3} – 3{x^2} – 9x + m} \right|\) trên đoạn \(\left[ { – 2;4} \right]\) bằng \(16\). Số phần tử của \(S\) là

Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.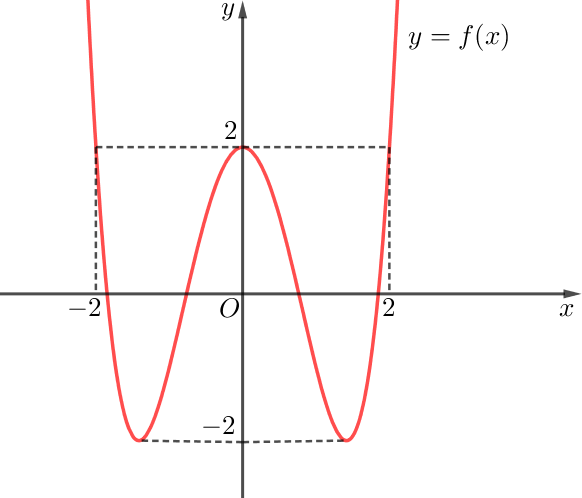

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ {0;20} \right]\) sao cho giá trị nhỏ nhất của hàm số \(g\left( x \right) = \left| {\left| {2f\left( x \right) + m + 4} \right| – f(x) – 3} \right|\) trên đoạn \(\left[ { – 2;2} \right]\) không bé hơn \(1\)?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ {0;20} \right]\) sao cho giá trị nhỏ nhất của hàm số \(g\left( x \right) = \left| {\left| {2f\left( x \right) + m + 4} \right| - f(x) - 3} \right|\) trên đoạn \(\left[ { - 2;2} \right]\) không bé hơn \(1\)? A. \(18\). B. … [Đọc thêm...] vềCho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ {0;20} \right]\) sao cho giá trị nhỏ nhất của hàm số \(g\left( x \right) = \left| {\left| {2f\left( x \right) + m + 4} \right| – f(x) – 3} \right|\) trên đoạn \(\left[ { – 2;2} \right]\) không bé hơn \(1\)?

Có bao nhiêu giá trị của tham số thực \(m\) để GTNN của hàm số \(y = \left| {{x^2} – 2x + m} \right| + 4x\) bằng \( – 1\)?-

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Có bao nhiêu giá trị của tham số thực \(m\) để GTNN của hàm số \(y = \left| {{x^2} - 2x + m} \right| + 4x\) bằng \( - 1\)? A. 0 B. 1 C. 2 D. 3 LỜI GIẢI CHI TIẾT Nếu \(m \ge 1\) thì \(y = {x^2} + 2x + m\) có GTNN là \(m - 1 = - 1 \Leftrightarrow m = 0\)(loại). Nếu \(m < 1\) thì \(y = \left\{ \begin{array}{l}{x^2} + 2x + m...\\ - {x^2} + 6x - … [Đọc thêm...] vềCó bao nhiêu giá trị của tham số thực \(m\) để GTNN của hàm số \(y = \left| {{x^2} – 2x + m} \right| + 4x\) bằng \( – 1\)?-

Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {\frac{1}{4}{x^4} + \frac{1}{3}\left( {{m^2} – 2} \right){x^3} – {m^2}{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,2} \right]\) luôn bé hơn hoặc bằng \(5\)?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {\frac{1}{4}{x^4} + \frac{1}{3}\left( {{m^2} - 2} \right){x^3} - {m^2}{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,2} \right]\) luôn bé hơn hoặc bằng \(5\)? A. \(0.\) B. \(4.\) C. \(7.\) D. \(8.\) LỜI GIẢI CHI TIẾT Xét hàm số \(g\left( x … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {\frac{1}{4}{x^4} + \frac{1}{3}\left( {{m^2} – 2} \right){x^3} – {m^2}{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,2} \right]\) luôn bé hơn hoặc bằng \(5\)?

Gọi S là tập hợp các giá trị của m để giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {{x^3} – 12x + m} \right|\) trên đoạn\(\left[ {1;3} \right]\) bằng 10. Tổng các giá trị của S là?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Câu hỏi: Gọi S là tập hợp các giá trị của m để giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {{x^3} - 12x + m} \right|\) trên đoạn\(\left[ {1;3} \right]\) bằng 10. Tổng các giá trị của S là? A. 10. B. 15. C. 20. D. 25. LỜI GIẢI CHI TIẾT \(\begin{array}{l}g(x) = {x^3} - 12x + m;\quad g'(x) = 3{x^2} - 12 = 0 \Leftrightarrow \left[ … [Đọc thêm...] vềGọi S là tập hợp các giá trị của m để giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {{x^3} – 12x + m} \right|\) trên đoạn\(\left[ {1;3} \right]\) bằng 10. Tổng các giá trị của S là?