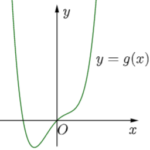
Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị.
A. \(2\). B. \(6\). C.\(5\). D. \(3\).
Lời giải
Xét hàm số \(g\left( x \right) = {x^4} + 2a{x^2} + 8x\); \(\mathop {\lim }\limits_{x \to \pm \infty } \,g\left( x \right) = + \infty \).
\(g\left( x … [Đọc thêm...] về Đề toán 2022 [2D1-2.7-4] Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị.
Kết quả tìm kiếm cho: ty so
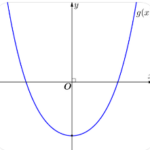
Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?
Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} - 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?
A. \(5\). B. \(6\). C. \(12\). D. \(11\).
Lời giải
Xét hàm số \(g\left( x \right) = {x^4} - 2m{x^2} + 64x\); \(\mathop {\lim }\limits_{x \to \pm \infty } g\left( x \right) = + \infty \)
\(g\left( x … [Đọc thêm...] về Đề toán 2022 [Mức độ 3] Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {{x^4} – 2m{x^2} + 64x} \right|\) có đúng ba điểm cực trị?
Đề toán 2022 [2D2-4.4-4] Xét tất cả các số thực \(x\), \(y\) sao cho \({49^{9 – {y^2}}} \ge {a^{4x – {{\log }_7}{a^2}}}\) với mọi số thực dương \(a\). Giá trị lớn nhất của biểu thức \(P = {x^2} + {y^2} + 4x – 3y\) bằng.
Đề toán 2022 [2D2-4.4-4] Xét tất cả các số thực \(x\), \(y\) sao cho \({49^{9 - {y^2}}} \ge {a^{4x - {{\log }_7}{a^2}}}\) với mọi số thực dương \(a\). Giá trị lớn nhất của biểu thức \(P = {x^2} + {y^2} + 4x - 3y\) bằng.
A. \(\frac{{121}}{4}\). B. \(\frac{{39}}{4}\). C. \(24\). D. \(39\).
Lời giải
+) Với mọi số thực dương \(a\), ta … [Đọc thêm...] về Đề toán 2022 [2D2-4.4-4] Xét tất cả các số thực \(x\), \(y\) sao cho \({49^{9 – {y^2}}} \ge {a^{4x – {{\log }_7}{a^2}}}\) với mọi số thực dương \(a\). Giá trị lớn nhất của biểu thức \(P = {x^2} + {y^2} + 4x – 3y\) bằng.
Đề toán 2022 [Mức độ 3] Có bao nhiêu số nguyên dương \(a\) sao cho ứng với mỗi \(a\) có đúng hai số nguyên \(b\) thỏa mãn \(\left( {{3^b} – 3} \right)\left( {a{{.2}^b} – 16} \right) < 0?\)
Đề toán 2022 [Mức độ 3] Có bao nhiêu số nguyên dương \(a\) sao cho ứng với mỗi \(a\) có đúng hai số nguyên \(b\) thỏa mãn \(\left( {{3^b} - 3} \right)\left( {a{{.2}^b} - 16} \right) < 0?\)
A. \(34\). B. \(32\). C. \(31\). D. \(33\).
Lời giải
Ta có: \(a \in {\mathbb{Z}^ + } \Rightarrow a \ge 1;\,b \in Z\)
\(\left( {{3^b} - 3} \right)\left( {a{{.2}^b} - 16} \right) … [Đọc thêm...] về Đề toán 2022 [Mức độ 3] Có bao nhiêu số nguyên dương \(a\) sao cho ứng với mỗi \(a\) có đúng hai số nguyên \(b\) thỏa mãn \(\left( {{3^b} – 3} \right)\left( {a{{.2}^b} – 16} \right) < 0?\)
Lý thuyết Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản – Toán 10 Cánh Diều
Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản - Toán 10 Cánh Diều ======= 1.1. Xác suất của biến cố trong trò chơi tung đồng xu Xác suất của biến cố A, kí hiệu P(A), là tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của không gian mẫu \(\Omega \): \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega … [Đọc thêm...] vềLý thuyết Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản – Toán 10 Cánh Diều
Lý thuyết Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm – Toán 10 Cánh Diều
Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm - Toán 10 Cánh Diều ======= Tóm tắt lý thuyết 1.1. Khoảng biến thiên, khoảng tứ phân vị a) Định nghĩa + Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó. Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau: \(R = … [Đọc thêm...] vềLý thuyết Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm – Toán 10 Cánh Diều
Lý thuyết Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm – Toán 10 Cánh Diều
Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm - Toán 10 Cánh Diều ======= 1.1. Số trung bình cộng (số trung bình) a) Định nghĩa Số trung bình cộng của một mẫu n số liệu thống kê bằng tổng của các số liệu chia cho số các số liệu đó. Số trung bình cộng của mẫu số liệu \({x_1},{x_2},...,{x_n}\) bằng \(\bar x = \frac{{{x_1} + … [Đọc thêm...] vềLý thuyết Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm – Toán 10 Cánh Diều
Lý thuyết Bài 1: Số gần đúng. Sai số – Toán 10 Cánh Diều
Bài 1: Số gần đúng. Sai số - Toán 10 Cánh Diều ======= Tóm tắt lý thuyết 1.1. Số gần đúng Trong đo đạc và tính toán, ta thường chỉ nhận được các số gần đúng. Ví dụ: a) Người ta thường lấy \(\pi \) xấp xỉ 3,14. Khi đó 3,14 là một số gần đúng của số đúng \(\pi \) b) Cho số \(\overline a = 2,17369266494051...\), thì số \(a = 2,1737\) là một số gần đúng của số đúng … [Đọc thêm...] vềLý thuyết Bài 1: Số gần đúng. Sai số – Toán 10 Cánh Diều
Lý thuyết Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây – Toán 10 Cánh Diều
Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây - Toán 10 Cánh Diều ======= 1.1. Quy tắc cộng Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành. Ví dụ: Bạn … [Đọc thêm...] vềLý thuyết Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây – Toán 10 Cánh Diều
Lý thuyết Bài 5: Tích của một số với một vectơ – Toán 10 Cánh Diều
Bài 5: Tích của một số với một vectơ - Toán 10 Cánh Diều ======= Tóm tắt lý thuyết 1.1. Định nghĩa +) Tích của một số thực \(k\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí kiệu là \(k\overrightarrow a .\) +) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với … [Đọc thêm...] vềLý thuyết Bài 5: Tích của một số với một vectơ – Toán 10 Cánh Diều