Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Cho hàm số \(y = \frac{{ – {x^2} + mx + m}}{{ – mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\)

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

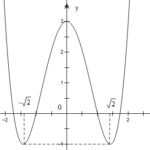
Đề bài: Cho hàm số \(y = \frac{{ - {x^2} + mx + m}}{{ - mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\) Lời giải $1$. Ta có:    \( \left\{ \begin{array}{l}- ymx + my =  - {x^2} + mx + m\\mx \ne m\end{array} … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{ – {x^2} + mx + m}}{{ – mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\)

Đề: Tính vi phân của mỗi hàm số sau : a) $y = \tan ^2 x$                              b) $ y = \sin x. \sin 2x $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tính vi phân của mỗi hàm số sau : a) $y = \tan ^2 x$                              b) $ y = \sin x. \sin 2x $ Lời giải a) Ta có ngay :       $ dy = y'dx = (\tan ^2 x)'dx = 2 \tan x . \frac{1}{\cos ^2 x }dx  = \frac{2 \tan  x. dx}{\cos ^2 x}$b) Ta có ngay :       $ dy = y'dx = ( \sin x . \sin 2x)'dx = (\cos x. \sin 2x + 2 \sin x . \cos 2x)dx$ … [Đọc thêm...] vềĐề: Tính vi phân của mỗi hàm số sau : a) $y = \tan ^2 x$                              b) $ y = \sin x. \sin 2x $

Đề: Tìm vi phân của các hàm số sau:a) $y=\frac{x+1}{x-2} $                                     b) $y=\frac{1}{0,5x^2} $                              c) $y=\frac{x^3+1}{x^3-1} $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm vi phân của các hàm số sau:a) $y=\frac{x+1}{x-2} $                                     b) $y=\frac{1}{0,5x^2} $                              c) $y=\frac{x^3+1}{x^3-1} $ Lời giải a) $-\frac{3dx}{(x-2)^2} $;                    b) $-\frac{4}{x^3}dx $;                          c)$-\frac{6x^2dx}{(x^3-1)^2} $ … [Đọc thêm...] vềĐề: Tìm vi phân của các hàm số sau:a) $y=\frac{x+1}{x-2} $                                     b) $y=\frac{1}{0,5x^2} $                              c) $y=\frac{x^3+1}{x^3-1} $

Đề:   Xác định tham số $a,b$ sao cho hàm số $y=\frac{ax+b}{x^2+1}$ đạt giá trị lớn nhất bằng $4$, giá trị nhỏ nhất bằng $-1$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:   Xác định tham số $a,b$ sao cho hàm số $y=\frac{ax+b}{x^2+1}$ đạt giá trị lớn nhất bằng $4$, giá trị nhỏ nhất bằng $-1$ Lời giải  GiảiTập xác định: $D=R$$y_0$ thuộc miền giá trị của hàm số khi và chỉ khi phương trình sau có nghiệm:      $y_0=\frac{ax+b}{x^2+1} \Leftrightarrow y_0x^2-ax+y_0-b=0    (1)$ -  Nếu $y_0=0$ thì $(1) \Leftrightarrow ax=-b$ có nghiệm … [Đọc thêm...] vềĐề:   Xác định tham số $a,b$ sao cho hàm số $y=\frac{ax+b}{x^2+1}$ đạt giá trị lớn nhất bằng $4$, giá trị nhỏ nhất bằng $-1$

Đề: Cho hàm số \(y = {x^4} – 4{x^3} + m\,\,\left( C \right)\)$1$. Khảo sát hàm số với \(m = 3\)$2$. Giả sử đồ thị $(C)$ cắt trục hoành tại $4$ điểm phân biệt . Hãy xác định  $m$ sao cho hình phẳng giới hạn bởi đồ thị $(C)$ và trục hoành có diện tích phần phía trên và phần phía dưới trục hoành bằng nhau.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số \(y = {x^4} - 4{x^3} + m\,\,\left( C \right)\)$1$. Khảo sát hàm số với \(m = 3\)$2$. Giả sử đồ thị $(C)$ cắt trục hoành tại $4$ điểm phân biệt . Hãy xác định  $m$ sao cho hình phẳng giới hạn bởi đồ thị $(C)$ và trục hoành có diện tích phần phía trên và phần phía dưới trục hoành bằng nhau. Lời giải $1$. Bạn đọc tự giải$2$. Giả sử đồ thị \(\left( {{C_m}} … [Đọc thêm...] vềĐề: Cho hàm số \(y = {x^4} – 4{x^3} + m\,\,\left( C \right)\)$1$. Khảo sát hàm số với \(m = 3\)$2$. Giả sử đồ thị $(C)$ cắt trục hoành tại $4$ điểm phân biệt . Hãy xác định  $m$ sao cho hình phẳng giới hạn bởi đồ thị $(C)$ và trục hoành có diện tích phần phía trên và phần phía dưới trục hoành bằng nhau.

Đề: Cho hàm số:  $f(x) = {x^4} + 2{x^2} + 2ax + {a^2} + 2a + 1$.a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $a = 0$.b) Xét các giá trị của $a$ để phương trình $f(x) = 0$ có nghiệm. Với mỗi $a$ đó, gọi ${x_a}$là nghiệm bé nhất của phương trình. Xác định $a$ để ${x_a}$ nhỏ nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $f(x) = {x^4} + 2{x^2} + 2ax + {a^2} + 2a + 1$.a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $a = 0$.b) Xét các giá trị của $a$ để phương trình $f(x) = 0$ có nghiệm. Với mỗi $a$ đó, gọi ${x_a}$là nghiệm bé nhất của phương trình. Xác định $a$ để ${x_a}$ nhỏ nhất. Lời giải a) Dành cho bạn đọc.b) Do ${x_a}$là nghiệm của $f(x) = 0$ nên$x_a^4 + … [Đọc thêm...] vềĐề: Cho hàm số:  $f(x) = {x^4} + 2{x^2} + 2ax + {a^2} + 2a + 1$.a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $a = 0$.b) Xét các giá trị của $a$ để phương trình $f(x) = 0$ có nghiệm. Với mỗi $a$ đó, gọi ${x_a}$là nghiệm bé nhất của phương trình. Xác định $a$ để ${x_a}$ nhỏ nhất.

Đề: Với $n$ là số nguyên dương cho trước, hãy biện luận theo $a$ số nghiệm của phương trình.                                         $\frac{{{x^{2n + 2}}}}{{2n + 2}} + \frac{{{x^{n + 2}}}}{{n + 2}} + \frac{{{x^2}}}{2} + a = 0$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Với $n$ là số nguyên dương cho trước, hãy biện luận theo $a$ số nghiệm của phương trình.                                         $\frac{{{x^{2n + 2}}}}{{2n + 2}} + \frac{{{x^{n + 2}}}}{{n + 2}} + \frac{{{x^2}}}{2} + a = 0$ Lời giải Viết lại phương trình đã cho dưới dạng:    $f\left( x \right) = \frac{{{x^{2n + 2}}}}{{2n + 2}} + \frac{{{x^{n + 2}}}}{{n + 2}} + … [Đọc thêm...] vềĐề: Với $n$ là số nguyên dương cho trước, hãy biện luận theo $a$ số nghiệm của phương trình.                                         $\frac{{{x^{2n + 2}}}}{{2n + 2}} + \frac{{{x^{n + 2}}}}{{n + 2}} + \frac{{{x^2}}}{2} + a = 0$

Đề: Trong các số thực $x, y, z$ thỏa mãn hệ thức \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 1} \right)^2} = 1\). Hãy tìm x, y, z để biểu thức \(|x + 2y + 3z – 8|\) đạt giá trị lớn nhất. Xác định giá trị đó.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Trong các số thực $x, y, z$ thỏa mãn hệ thức \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 1\). Hãy tìm x, y, z để biểu thức \(|x + 2y + 3z - 8|\) đạt giá trị lớn nhất. Xác định giá trị đó. Lời giải \(|x + 2y + 3z - 8|\)\( = |\left( {x - 1} \right) + 2\left( {y - 2} \right) + 3\left( {z - 1} \right)| \le \sqrt … [Đọc thêm...] vềĐề: Trong các số thực $x, y, z$ thỏa mãn hệ thức \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 1} \right)^2} = 1\). Hãy tìm x, y, z để biểu thức \(|x + 2y + 3z – 8|\) đạt giá trị lớn nhất. Xác định giá trị đó.

Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{2{x^2} + x}}{{x + 1}}\left( H \right)\)$2$. Tìm những điểm $M$ trên $y = 1$ sao cho từ $M$ có thể kẻ được đúng $1$ tiếp tuyến đến $(H)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{2{x^2} + x}}{{x + 1}}\left( H \right)\)$2$. Tìm những điểm $M$ trên $y = 1$ sao cho từ $M$ có thể kẻ được đúng $1$ tiếp tuyến đến $(H)$ Lời giải $1$. Bạn đọc tự giải:$2$. Xét \(M\left( {{x_0},1} \right)\) thuộc đường thẳng $y = 1$. Đường thẳng qua $M$, hệ số góc $k$ có phương trình \(y = k\left( {x - … [Đọc thêm...] vềĐề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{2{x^2} + x}}{{x + 1}}\left( H \right)\)$2$. Tìm những điểm $M$ trên $y = 1$ sao cho từ $M$ có thể kẻ được đúng $1$ tiếp tuyến đến $(H)$

Đề: Cho hàm số :  $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max  y , min  y.$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số :  $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max  y , min  y.$ Lời giải Tập xác định của hàm số là $R$     $y=1+\cos x + \frac{ 1}{ 2} (2 \cos ^2x -1)+\frac{ 1}{ 3} (4 \cos ^3 x -3 \cos x )$        $= \frac{ 4}{ 3} \cos ^3 x +\cos ^2 x +\frac{ 1}{ 2}  $Đặt $\cos x =t,$ với mọi $x$ thì $|t| \leq 1   (A)$Hàm số có dạng $f(t) = … [Đọc thêm...] vềĐề: Cho hàm số :  $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max  y , min  y.$